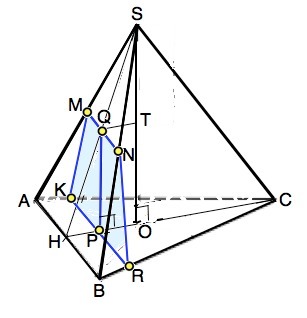
В правильной треугольной пирамиде SABC сторона основания AB равна 2√3, а боковое ребро SA равно 4. Точки M и N — середины рёбер SA и SB соответственно. Плоскость α содержит прямую MN и перпендикулярна плоскости основания пирамиды. Найдите площадь многоугольника, являющегося сечением пирамиды SABC плоскостью α.
Ответы
В основании правильной пирамиды лежит правильный многоугольник, а вершина пирамиды проецируется в центр основания.
Основание данной пирамиды - равносторонний треугольник АВС, боковые грани - равнобедренные треугольники. SO - высота, О - центр основания.
M и N — середины рёбер SA и SB, => MN- средняя линия ∆ ASB.
MN║AB=> MN║ABC
Плоскость α содержит прямую MN и перпендикулярна плоскости основания пирамиды. =>
Плоскость сечения перпендикулярна АВС. Для её построения из середины Q отрезка MN опустим перпендикуляр QP на плоскость АВС.
QP║SO, Р принадлежит высоте основания СН.
Прямая KR- линия пересечения плоскости альфа и АВС. Плоскость КМNR содержит прямую QP, перпендикулярную АВС => она перпендикулярна АВС ( свойство).
КМNR - сечение, площадь которого нужно найти, и является трапецией.
Площадь трапеции равна произведению её высоты на полусумму оснований.
S(KMNR)=QP•(MN+KR):2
Высота трапеции QP║ЅО, MN как средняя линия ∆ АЅВ делит апофему ЅН пополам. ⇒ QP - средняя линия ∆ ЅНО и равна половине SO.
ОС- высота и медиана ∆ АВС, О - центр ∆ АВС и делит СН в отношении 2:1
ОH =ВС•sin60°= 2√3•(√3/2)=3
OC=2, OH=1
Из прямоугольного ∆ ЅОС по т.Пифагора ЅО=√(SC*-OC*)=√(16-4)=2√3 => QP=√3
В прямоугольном ∆ ЅОН , где QP- средняя линия, НР=РО=1:2=0,5
Тогда СР=СО+ОР=2+0,5=2,5
KR|║AB
∆ КСR- равносторонний, все его углы 60°.
KR=CR=CP:sin60°=2,5:(√3/2)=5/√3=5√3/3
MN=AB:2=√3
S(KMNR)=0,5•[√3+(5√3/3)•√3=4 (ед. площади)