Предмет: Геометрия,
автор: mircomuz
В прямоугольном треугольнике биссектриса прямого угла делит гипотенузу в отношении 3:2. Найдите отношения проекций катетов на гипотенузу.
mircomuz:
Можете подробнее описать
Спасибо!)
Ответы
Автор ответа:
3
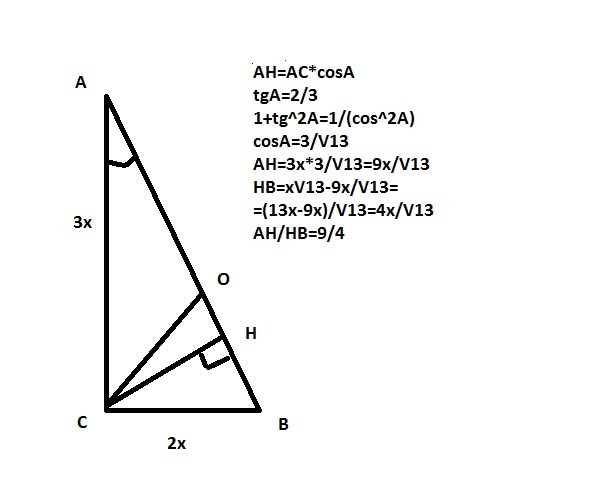
один катет 3х, другой 2х
Тогда гипотенуза x√13
Приложения:
Автор ответа:
3
Биссектриса треугольника делит противоположную сторону на части, пропорциональные прилежащим сторонам.
a/b =3/2 (a, b - катеты).
Высота из прямого угла делит гипотенузу на отрезки Ca=a^2/c; Cb=b^2/c (Сa, Cb - проекции катетов).
Ca/Cb =a^2/b^2 =(3/2)^2 =9/4
Приложения:
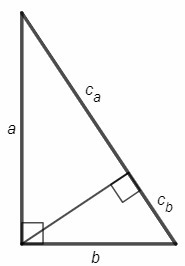
Высота из прямого угла делит треугольник на подобные друг другу и исходному, c/a=a/Ca => катет есть среднее пропорциональное между гипотенузой и проекцией катета на гипотенузу, a^2=Ca*c.
Похожие вопросы
Предмет: Математика,
автор: Аноним
Предмет: Другие предметы,
автор: daryasa322
Предмет: Информатика,
автор: molotovcherry
Предмет: Алгебра,
автор: Дуся2112
Предмет: Геометрия,
автор: morhalo2015