Предмет: Математика,
автор: 21WAR
Помогите ! Не могу решать
Приложения:
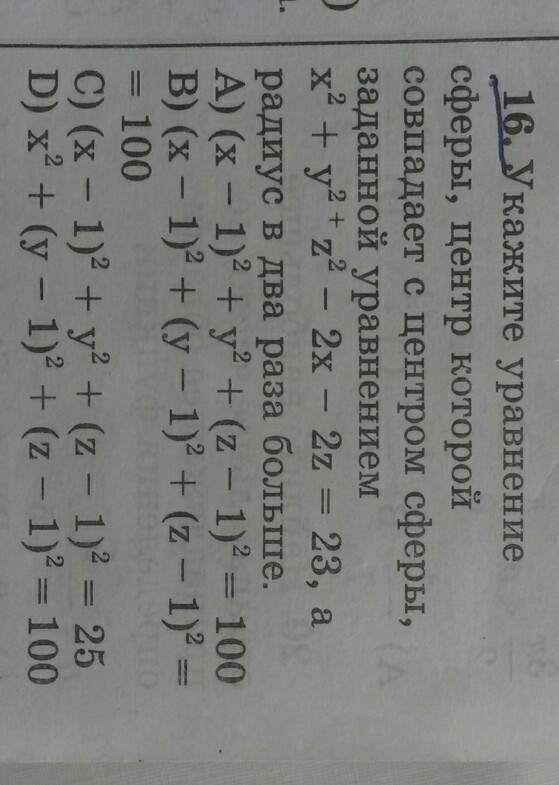
Ответы
Автор ответа:
0
Уравнение сферы:
Где R - радиус, (x₀, y₀, z₀) - координаты центра
Приводим уравнение нашей сферы к виду выше, для этого выделяем полные квадраты:
Радиус нашей сферы R=5
Радиус искомой сферы в 2 раза больше, то есть 10
Если центры совпадают, то ее уравнение:
ОТВЕТ: А)
Автор ответа:
0
х²+у²+z²-2x-2z=23
(x²-2x+1)+y²+(z²-2z+1)=23+2
(x-1)²+(y-0)²+(z-1)²=5²
A(1;0;1) ;r=5
R=2•r=10
(x-1)²+y²+(z-1)²=10²
(x-1)²+y²+(z-1)²=100
ответ А)
(x²-2x+1)+y²+(z²-2z+1)=23+2
(x-1)²+(y-0)²+(z-1)²=5²
A(1;0;1) ;r=5
R=2•r=10
(x-1)²+y²+(z-1)²=10²
(x-1)²+y²+(z-1)²=100
ответ А)
Похожие вопросы