Предмет: Алгебра,
автор: Mariaglu2
розвязати нерівність
Приложения:
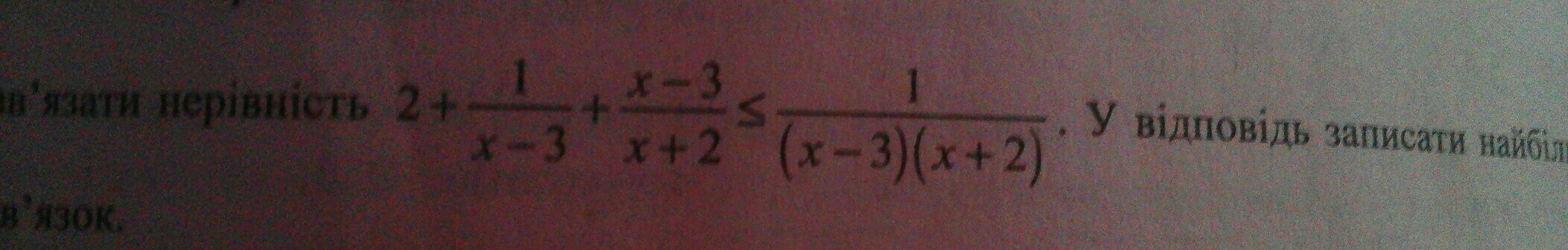
Ответы
Автор ответа:
2
Х не равен 3 и -2
Методом интервалов находим промежуток и накладывая то ,чему не равен х :
Автор ответа:
0
!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
Приложения:

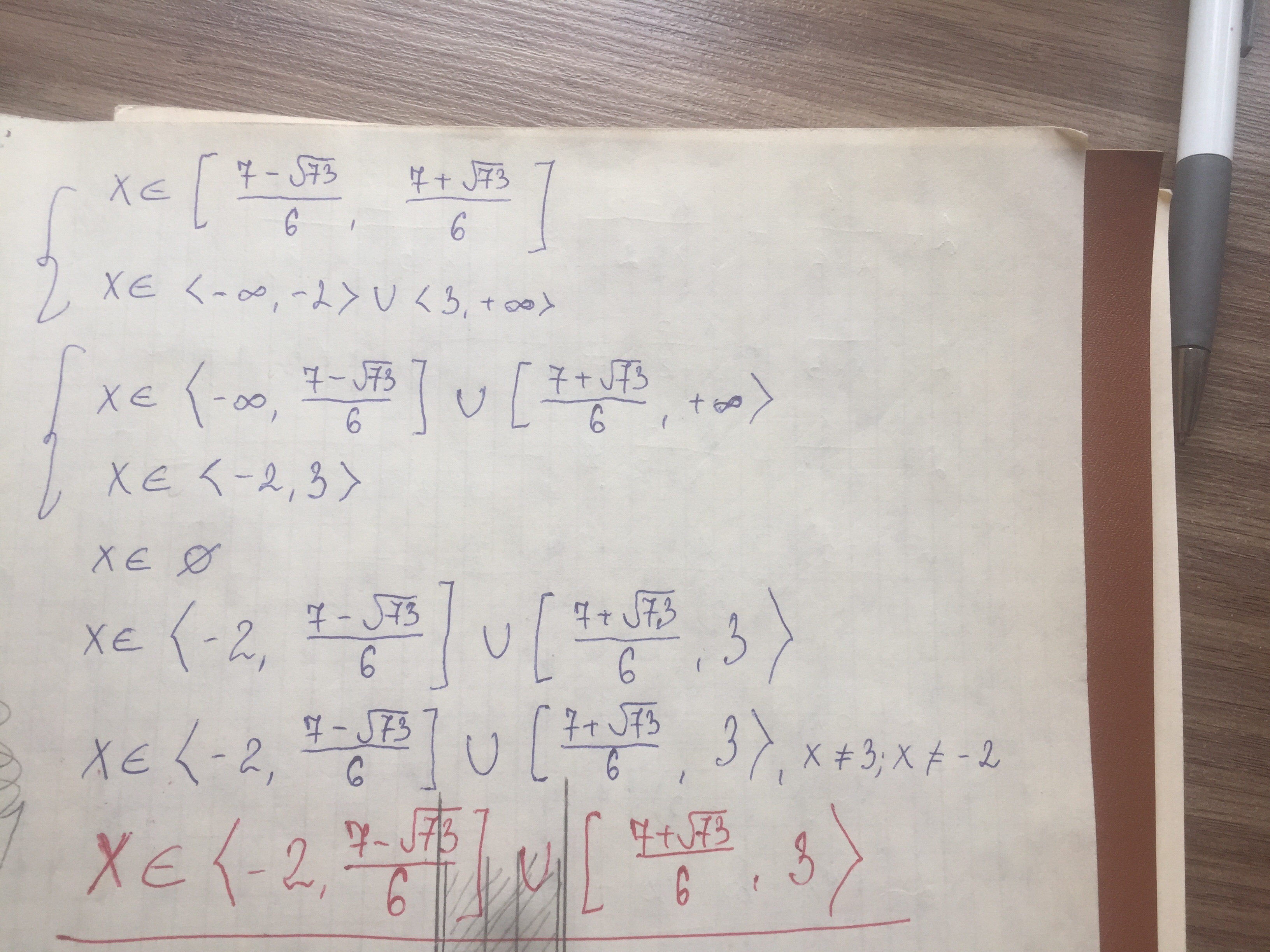
Похожие вопросы
Предмет: Геометрия,
автор: berlinvv154
Предмет: Алгебра,
автор: babuskinnikita2007
Предмет: Русский язык,
автор: nikitafart23
Предмет: Геометрия,
автор: Аноним
Предмет: Геометрия,
автор: asanovagalina