Предмет: Математика,
автор: ivanirkutov
Найти все значения параметра а, при который уравнение имеет решение.
Приложения:
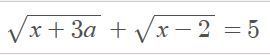
Ответы
Автор ответа:
0
В левой части уравнения стоит непрерывная, монотонно возрастающая функция с областью определения [max(2, -3a), +∞). При увеличении x её значения становятся больше 5, тогда, чтобы у уравнения было решение, значение этой функции в левой точке области определения x = max(2, -3a) должно быть не больше 5.
Если 2 ≥ -3a (a ≥ -2/3), то область определения функции [2, +∞). Значение в точке x = 2:
Если a ≤ -2/3, то область определения функции [-3a, +∞). Значение в точке -3a:
Ответ – объединение этих двух промежутков.
Ответ:
Похожие вопросы
Предмет: Математика,
автор: mbuyuvov
Предмет: Математика,
автор: vtaranenko954
Предмет: ОБЖ,
автор: Аноним
Предмет: Обществознание,
автор: wdghjlfv