Предмет: Математика,
автор: 04RoHamito
Помогите пожалуйста, найдити произведение корней уравнения х^3-3х^2-6х+8=0
тто:
х^3-3х^2-6х+8=0; (х+2)(х-1)(х-4)=0; х+2=0;х=-2;х-1=0;х=1;х-4=0;х=4.
Ответы
Автор ответа:
0
По теореме Виета для кубического уравнения ax^3+bx^2+cx+d=0
x1*x2*x3 = -d/a
В нашем случае: x1*x2*x3 = -8/1 = -8.
2 способ.
Будем раскладывать на скобки.
Проверим корень x = 1.
1 - 3 - 6 + 8 = -2-6+8 = -8+8 = 0, всё верно => x = 1 -- корень.
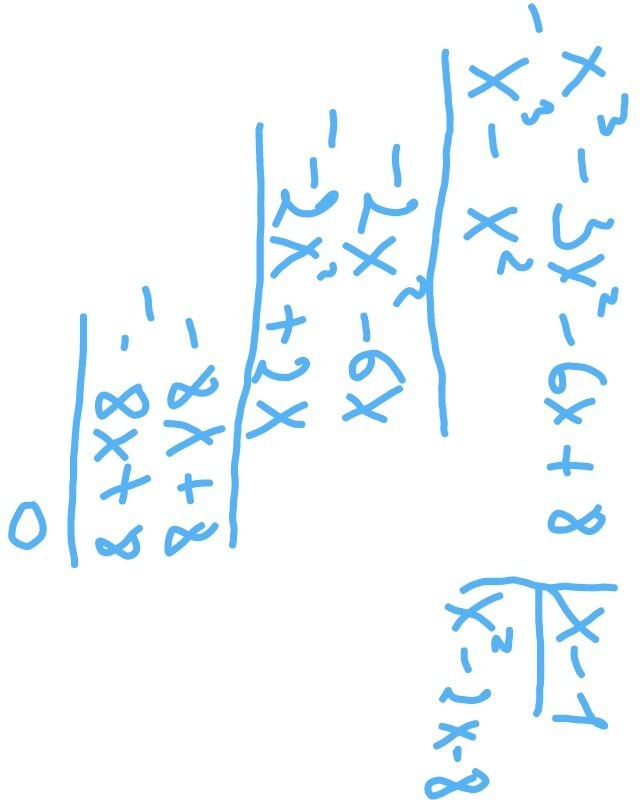
Поделим уравнение на (x-1): см.приложение.
Получаем: (x-1)*(x^2-2x-8) = 0
x^2-2x-8=0
x1 = 4
x2 = -2
x3 = 1
=> 4*(-2)*1 = -8
x1*x2*x3 = -d/a
В нашем случае: x1*x2*x3 = -8/1 = -8.
2 способ.
Будем раскладывать на скобки.
Проверим корень x = 1.
1 - 3 - 6 + 8 = -2-6+8 = -8+8 = 0, всё верно => x = 1 -- корень.
Поделим уравнение на (x-1): см.приложение.
Получаем: (x-1)*(x^2-2x-8) = 0
x^2-2x-8=0
x1 = 4
x2 = -2
x3 = 1
=> 4*(-2)*1 = -8
Приложения:
Похожие вопросы