Предмет: Математика,
автор: Schwarz78
Можете решить предел, пожалуйста НЕ через Лопиталя
Приложения:
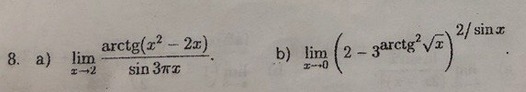
Аноним:
ну тут замечательные пределы
я вообще не понимаю, что с ними делать. И как ; -; я попытался, но вообще ни в какую, не приняли
через замечательные - вышло t/3pi (подстановка x=t-2) и 0. А через Лопиталя - 2/3pi и 1/9. Но лопиталя мы еще не проходили и поэтому преподаватель ругался и не принял.
В первом примере нужно перейти к эквивалентным бесконечно малым.
Ответы
Автор ответа:
0
a) Заменяя бесконечно малые arctg(x²-2*x) и sin(3*π*x) эквивалентными бесконечно малыми x²-2*x и 3*π*(x-2), получаем:
lim(x⇒2) arctg(x²-2*x)/sin(3*π*x)=lim(x⇒2) (x²-2*x)/[3*π*(x-2)]=1/(3*π)*lim(x⇒2) x=2/3*π. Ответ: 2/(3*π).
а тригонометрические функции можно вот так просто заменить? странно, а зачем они тогда вообще нужны в пределе, если они ни на что не влияют?
и почему при замене арксинуса ничего не поменялось, а при замене с синуса x стал x-2?
1. При вычислении предела любую бесконечно малую можно заменить эквивалентной. 2. Арксинуса в первом задании нет, есть арктангенс. А x-2 нужно затем, чтобы величина 3*pi*(x-2) была бесконечно малой при x ->0.
Вернее, при x->2.
перепутал, простите. Но так и не понятно, почему у синуса происходит замена переменной, а у арктангенса нет
Потому что 3*pi*x не стремится к 0 при x->2 - следовательно, не является бесконечно малой при x->2. А вот 3*pi*(x-2) является.
Похожие вопросы
Предмет: Геометрия,
автор: kot9paLox
Предмет: Английский язык,
автор: pomiidor
Предмет: Химия,
автор: Kerteker
Предмет: Физика,
автор: irinaaaaaaaaaaaaa
Предмет: Экономика,
автор: shunin100