Предмет: Геометрия,
автор: Vadim03022000
В кубе ABCDA1B1C1D1 на ребре AA1 взята точка M такая, что AM=2MA1......ребре BC - точка N такая, что BN = 3NC. Найти косинус угла между ..... MN и AC1.
Помогите решить, пожалуйста. С рисунком.
Ответы
Автор ответа:
1
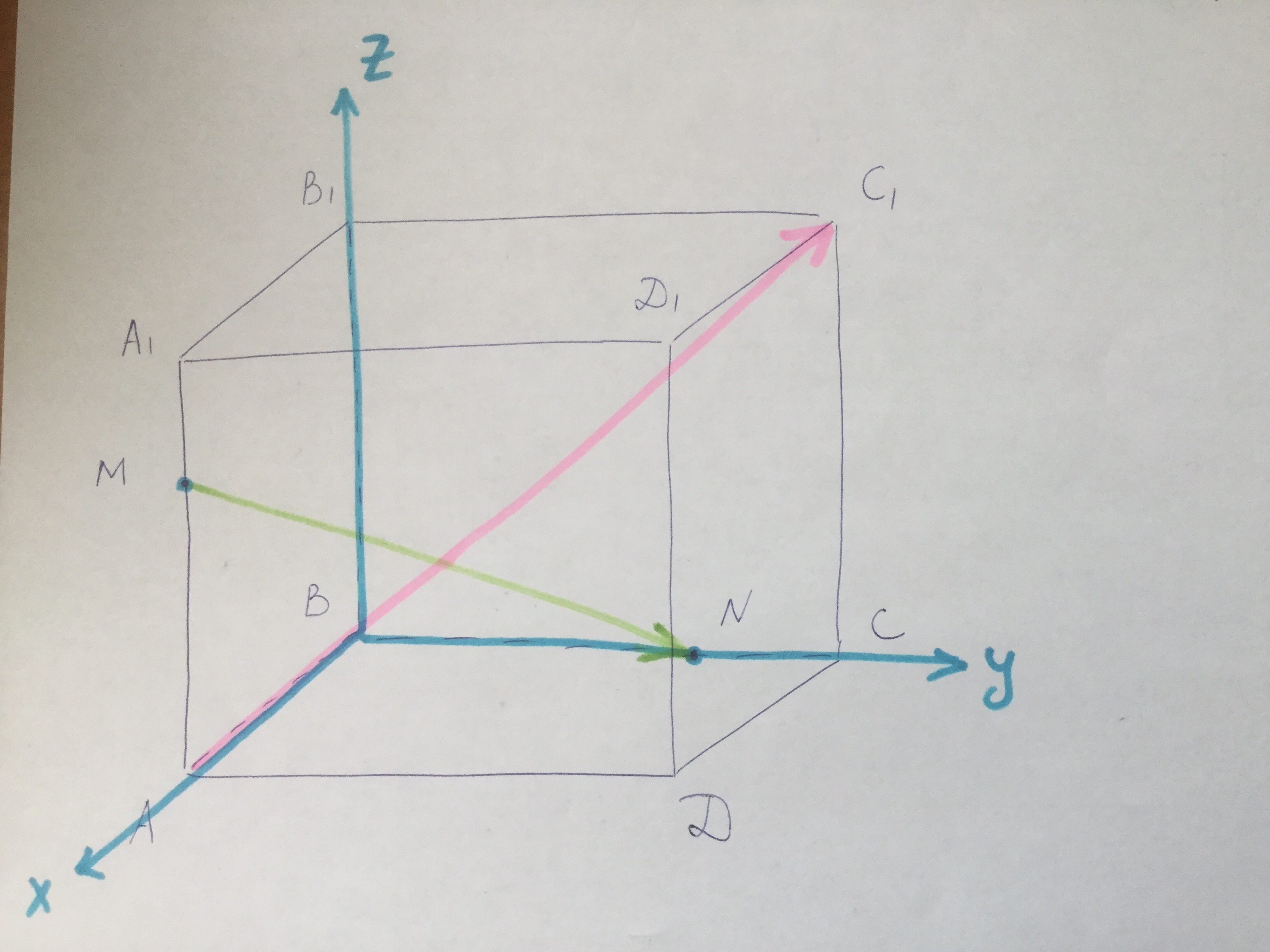
Введём трёхмерную систему координат с началом в точке В таким образом, что ось Х совпадает с ребром ВА, ось Y -- с ребром ВС, ось Z -- с ребром ВВ₁.
Длину ребра куба положим равной 12 (12 делится нацело и на 3, и на 4), чтобы не только вершины куба, но и точки M и N имели целочисленные координаты.
Определим координаты точек M, N, A и С₁:
M (12; 0; 8), N (0; 9; 0), A (12; 0; 0), С₁ (0; 12; 12).
Определим координаты векторов MN и AС₁:
MN (-12; 9; -8), AС₁ (-12; 12; 12).
cos φ = MN·AС₁ / |MN|·|AС₁| = -12·(-12)+9·12-8·12 / √((-12)²+9²+(-8)²)·√((-12)²+12²+12²) = 12·13 / 17·12√3 = 13/17√3 = 13√3/51
Приложения:
Похожие вопросы
Предмет: Химия,
автор: perviyigrok245
Предмет: Другие предметы,
автор: sereniti91
Предмет: Биология,
автор: erikamusic
Предмет: Алгебра,
автор: story12