Question

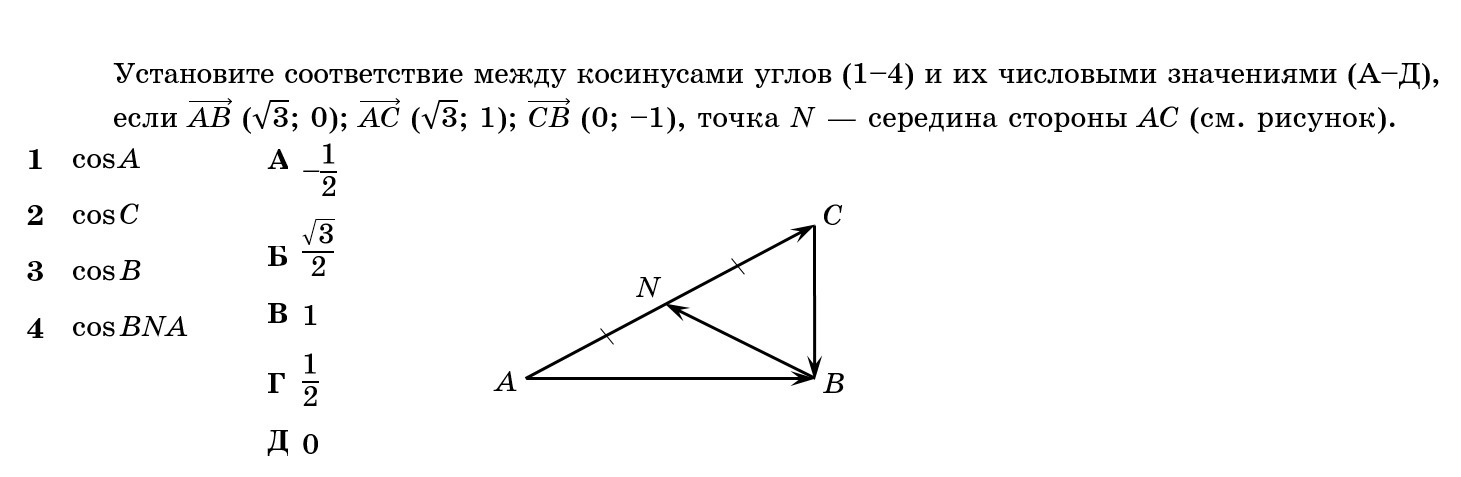
Помогите, с геометрией (см. фото).

Answer 1

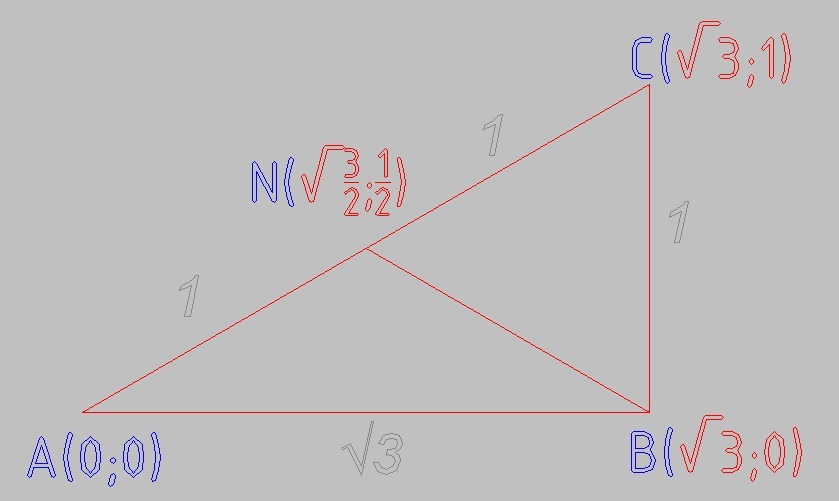
|AC| = √(√3² + 1²) = √(3 + 1) = √4 = 2

|NC| = |AN| = 2/2 = 1

---

|BC| = √((√3 - √3)² + (1 - 0)²) = √(0 + 1) = √1 = 1

---

Треугольник BNC - равносторонний, ∠BNC = 60°

--- 4 ---

∠ANB = 180 - ∠BNC = 180 - 60 = 120°

cos(120°) = - 1/2

--- 1 ---

в равнобедренном ΔANB

∠A = (180 - ∠ANB)/2 = (180 - 120)/2 = 30°

cos(30°) = √3/2

--- 3 ---

∠B = ∠NBA + ∠NBC = 30° + 60° = 90°

cos(90°) = 0

--- 2 ---

в прямоугольном ΔАВС

∠С = 90 - ∠А = 60°

cos(60°) = 1/2

(пункты пронумерованы по мере их решения)

Answer 2

Если задачу надо решить в векторном виде, то для нахождения косинусов, воспользуемся формулой:

$cos\alpha =\frac{\vec{a}*\vec{b}}{|\vec{a}|*|\vec{b}|}$

cosBNA - это косинус между векторами NA и NB

$\vec{AN}=\frac{\vec{AC}}{2} =(\frac{\sqrt{3}}{2} ;\frac{1}{2} )$

векторы складываются и вычитаются по правилу треугольника, поэтому:

$\vec{BN}=\vec{AN}-\vec{AB}=(\frac{\sqrt{3}}{2} -\sqrt{3} ; \frac{1}{2} -0)=(-\frac{\sqrt{3}}{2} ; \frac{1}{2})\\ \\ \vec{NA}=-\vec{AN}=(-\frac{\sqrt{3}}{2} ; -\frac{1}{2})\\ \\ \vec{NB}=-\vec{BN}=(\frac{\sqrt{3}}{2} ;- \frac{1}{2}) \\ \\ cosBNA=\frac{\vec{NA}*\vec{NB}}{|\vec{NA}|*|\vec{NB}|} =\frac{-\frac{\sqrt{3}}{2}*\frac{\sqrt{3}}{2}+\frac{1}{2}*\frac{1}{2}}{\sqrt{(-\frac{\sqrt{3}}{2})^2+(-\frac{1}{2})^2}*\sqrt{(\frac{\sqrt{3}}{2})^2+(-\frac{1}{2})^2}} = \\ \\ =$

$=\frac{-\frac{3}{4}+\frac{1}{4}}{\sqrt{\frac{3}{4}+\frac{1}{4}}*\sqrt{\frac{3}{4}+\frac{1}{4}}}=\frac{-\frac{2}{4}}{1*1} =-\frac{1}{2} \\ \\ OTBET: \ 4-A$