Предмет: Алгебра,
автор: 138138123AAA
Помогите решить подробно логарифм. Спасибо
Приложения:
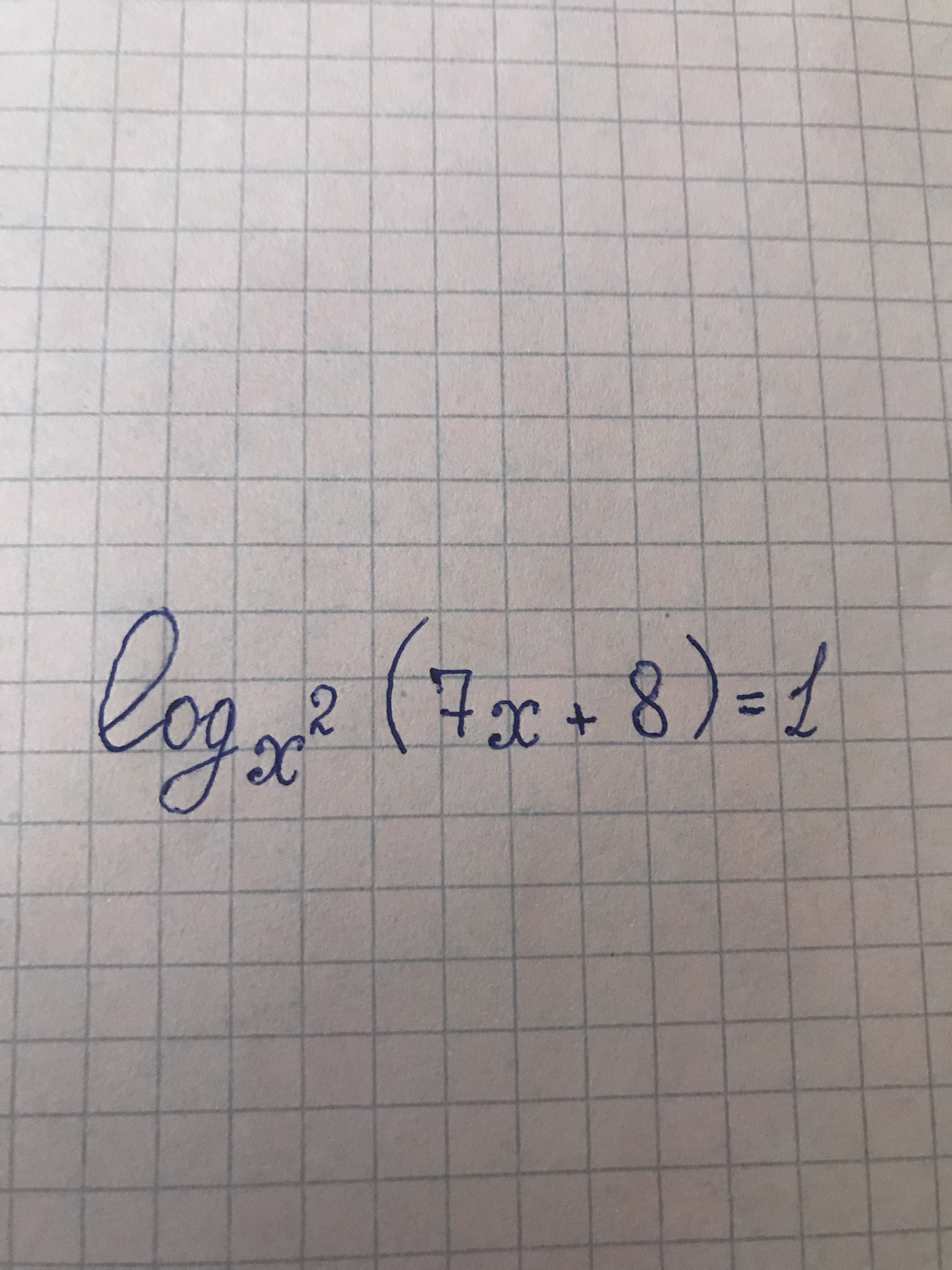
Ответы
Автор ответа:
1
Здесь должен быть знак перечёркнутого равно
х принадлежит
-1 - посторонний корень
Ответ : х=8
Автор ответа:
1
Находим все значения х, которые дают отрицательное или равное 1 основание.
х²≤0
х²=1
Находим все значения х, которые дают отрицательный аргумент логарифма.
7х+8≤0
Решим неравенство относительно х.
х∈[0;0]
х=1
х=-1
х≤-8/7
Находим объединение. Чтобы найти область допустимых значений, нужно удалить исключенные значения.
х∈(-8/7; -1)∪(-1;0)∪(0;1)∪(1;+∞)
Решим уравнение путём преобразования логарифма в степень, т.е. log(внизу а) (х)=b равно x=a(b вверху)
7х+8=(х²)¹
7х+8=х²
-х²+7х+8=0
х²-7х-8=0
х1,2=(-b+-√D)/2a
D=b²-4ac=(-7)²-4*1*(-8)=49+32=81
√81=9
х1=(7-9)/2*1=-2/2=-1
х2=(7+9)/2=16/2=8
х∈(-8/7; -1)∪(-1;0)∪(0;1)∪(1;+∞)
Заключительное действие: проверим, принадлежит ли решение заданному интервалу.
х=8
Похожие вопросы