Предмет: Алгебра,
автор: qwerty3597
решите уравнение логарифмы
Приложения:
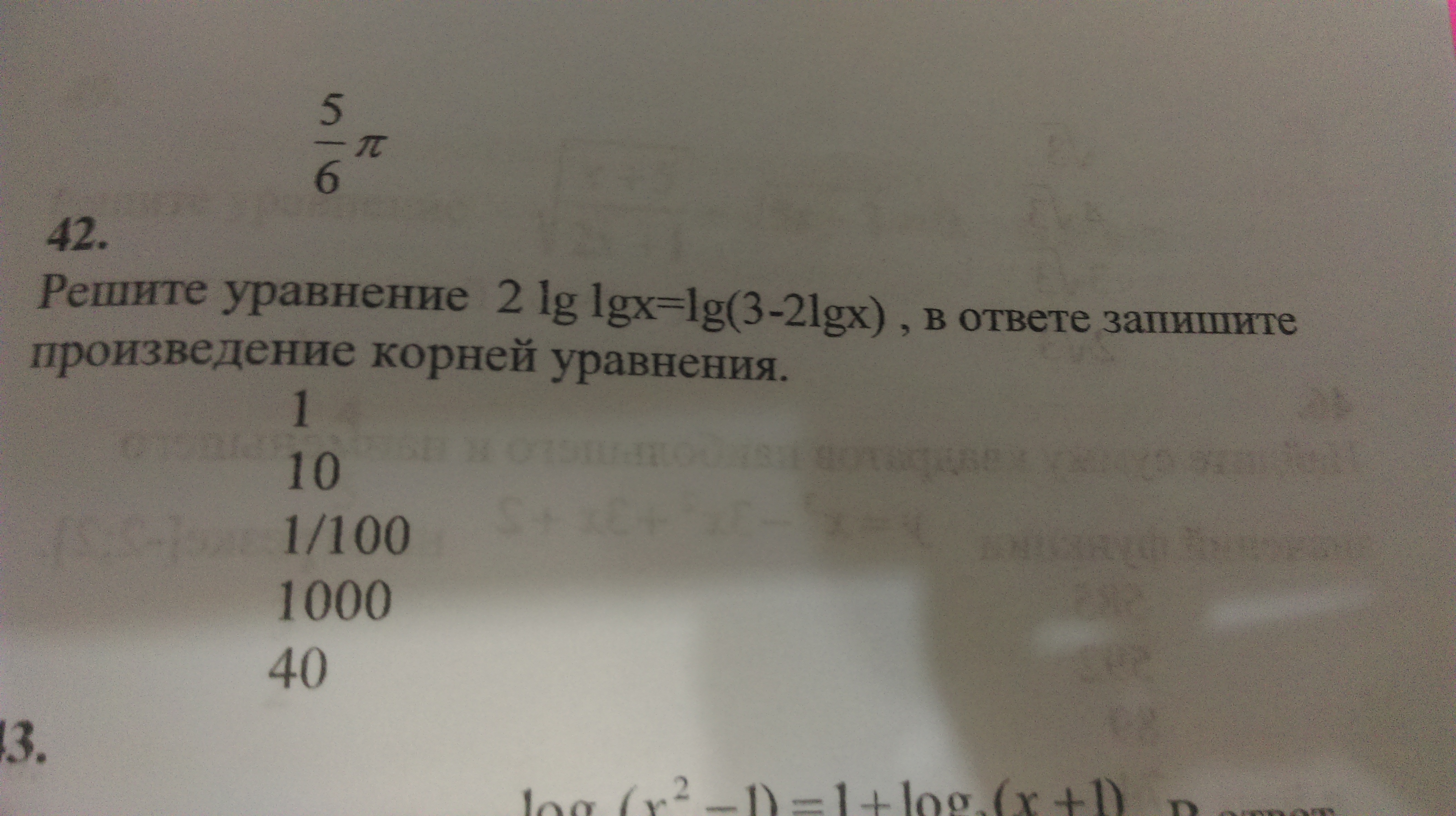
AlfaAndOmega:
1/100
Ответы
Автор ответа:
1
одз: x>0
2 lg lgx = lg(3-2lgx)
lg (lgx)²= lg(3-2lgx)
lg²x = 3-2lgx
lg²x + 2lgx - 3 = 0
Введем замену lgx = t
t² + 2t - 3 = 0
D = 4 - 4*1*(-3) = 16
t1 = (-2+4)/2 = 1
t2 = (-2-4)/2 = -3
Вернемся к замене:
lgx = 1
x = 10
lgx = -3
x = 10⁻³ = 1/1000
10* 1/1000 = 1/100
2 lg lgx = lg(3-2lgx)
lg (lgx)²= lg(3-2lgx)
lg²x = 3-2lgx
lg²x + 2lgx - 3 = 0
Введем замену lgx = t
t² + 2t - 3 = 0
D = 4 - 4*1*(-3) = 16
t1 = (-2+4)/2 = 1
t2 = (-2-4)/2 = -3
Вернемся к замене:
lgx = 1
x = 10
lgx = -3
x = 10⁻³ = 1/1000
10* 1/1000 = 1/100
loga(b) = c, с может быть отрицательным
b нет
Всё верно
У меня положительные иксы все
Не знаете -- не лезьте.
А, понял.
Извините.
Умник здесь изначально ОДЗ: lg(x)>0 и 3-2lg(x)>0....Это ты не учёл??????
Я уже осознал и извинился.
...
Автор ответа:
1
Ответ:..................................
Приложения:
Почему lgx>0?
это неверная запись
10^(-3) = 1/1000, почему нет?
loga(b)=c одз>0
lga=c одз a>0 в первой строке lgx является a для 2lglgx и поэтому согласно одз должен быть >0
lga=c одз a>0 в первой строке lgx является a для 2lglgx и поэтому согласно одз должен быть >0
А, сорян
Похожие вопросы
Предмет: Обществознание,
автор: Kolibrik777
Предмет: Литература,
автор: anoska
Предмет: Химия,
автор: sofiaskakun582
Предмет: Музыка,
автор: ghjk455