Предмет: Математика,
автор: nata97971
Стороны треугольника равны 55, 55, 66 см. Найти площадь треугольника, вершинами которого служат основания биссектрис данного треугольника.
LerroyJay:
h=√(55^2-(66/2)^2)=44; S=44*66/2=1452
Площадь не того треугольника я посчитал))) h/33=tg(a/2)=sin(a)/(1+cos(a))=(44/55)/(1+33/55)=(4/5)/(8/5)=1/2; h=33/2=16,5; Пусть основание будет x, тогда (44-16,5)/x=44/66; x=66*27,5/44=41,25. S=41,25*16,5/2=340,3125
Ответы
Автор ответа:
2
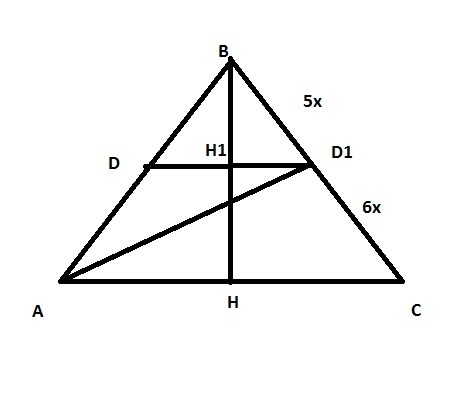
Надо найти S ΔDD1H=DD1*HH1/2
Биссектриса делит противоположную сторону пропорционально прилежащим сторонам в треугольнике
AD1 делит ВС на BD1= 5х и D1C=6х
5х+6х=11х=55; x=5; BD1=25; D1C=30
треугольники НВС и Н1ВD1 подобны по 2 углам с k=11/5
H1D1=HC/k=33/(11/5)=15
HD=2H1D1=30
BH^2=BC^2-HC^2=55^2-33^2=44^2; BH=44
HH1=HB-BH1=44-HB/(11/5)=44-44/(11/5)=44-20=24
S=30*24/2=360
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: shmygaveronika
Предмет: Математика,
автор: jajjaja11037
Предмет: Алгебра,
автор: KaguaOotsutsuki
Предмет: Математика,
автор: ThegemsBOBE
Предмет: Химия,
автор: uchenitsaKatya