Question

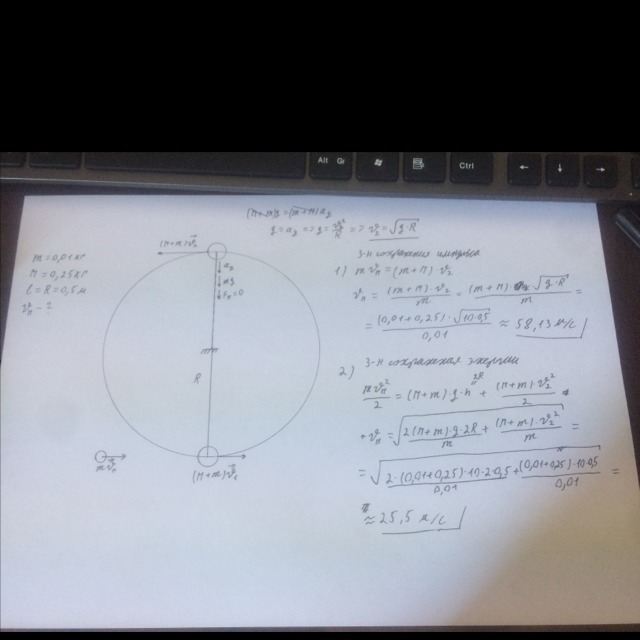
Пуля массой 0,01кг абсолютно неупруго врезается в груз массой 0,25кг, висящий на невесомой нити длинной 0,5м. Найти минимальную скорость пули, при которой груз сделает полный оборот.

Answer 1

запишем закон сохранения импульса, учитывая, что соударение абсолютно неупругое (пуля с грузом после соударения движутся как единое целое):

m v = (m + M) u,

u = v [m/(m+M)] - скорость пули и груза после соударения.

запишем закон сохранения энергии для начального положения (h = 0) и конечного в наивысшей точке подъема (h' = 2L, где L - длина нити). примем для простоты записи m' = m + M:

(m' u²)/2 = (m' V²)/2 + m'g2L, где V - скорость пули с грузом на высоте 2L.

запишем уравнение динамики для пули с грузом на высоте 2L:

m'g + T = m'a.

скорость v минимальна в том случае, когда T = 0. учитывая, что движение происходит по окружности, получим g = V²/L. поэтому V = √[gL]. тогда в ЗСЭ будем иметь:

(v [m/(m+M)])² = gL + 4 gL

(v [m/(m+M)])² = 5 gL

v = [(m+M)/m)] * sqrt(5gL)

v = ((0.01+0.25)/(0.01))*sqrt(50*0.5) = 130 м/c