Предмет: Алгебра,
автор: yudinaira4444
объясните, как решать подобное
Приложения:
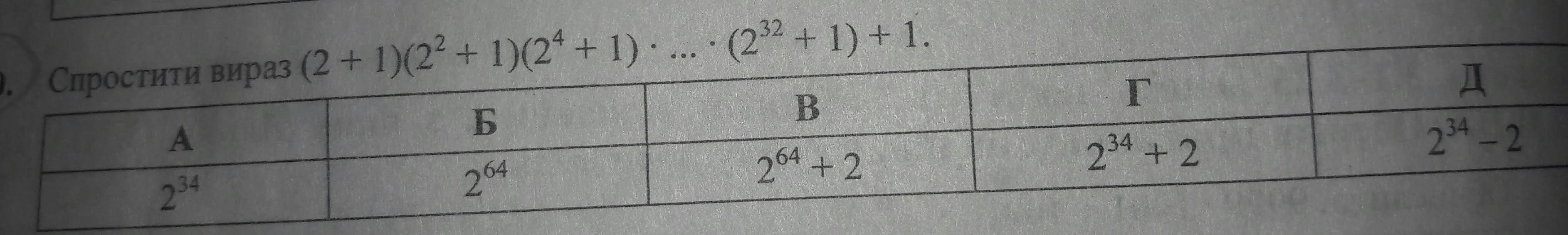
Ответы
Автор ответа:
1
NeZeRAvix:
домножаем все на (2-1)=1, далее разность квадратов
Похожие вопросы
Предмет: Математика,
автор: arishkasava
Предмет: Русский язык,
автор: texamer
Предмет: Қазақ тiлi,
автор: davletnazarovatilekt
Предмет: Геометрия,
автор: МарьянаРо14
Предмет: Информатика,
автор: quard123