Предмет: Алгебра,
автор: NeoBest1
Помогите решить логарифмическое уравнение
Приложения:
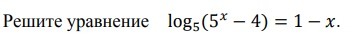
Ответы
Автор ответа:
1
5^(1-х)=5^х-4
5/5^х=5^х-4
5^х=t
5/t=t-4
t^2-4t-5=0
D/4=4+5=9
t1=2+3=5
t2=2-3=-1 (лишний корень)
5^х=5
х=1
Автор ответа:
0
решая уравнение относительно , раскладываем на множители:
что больше – или
?
при основании больше единицы логарифм тем больше, чем больше его показатель (, поэтому
)
yugolovin:
У Вас не выписан окончательный ответ
Кстати, проверку x>log_5 4 в такой задаче можно не делать, ведь 5^x-4 равно 5 в некоторой степени. И поэтому 5^x-4>0 автоматически
Похожие вопросы
Предмет: Русский язык,
автор: momotnazar031
Предмет: Немецкий язык,
автор: novikov09
Предмет: Химия,
автор: timsit234
Предмет: Экономика,
автор: SmileSky20
Предмет: Химия,
автор: aienka