Question

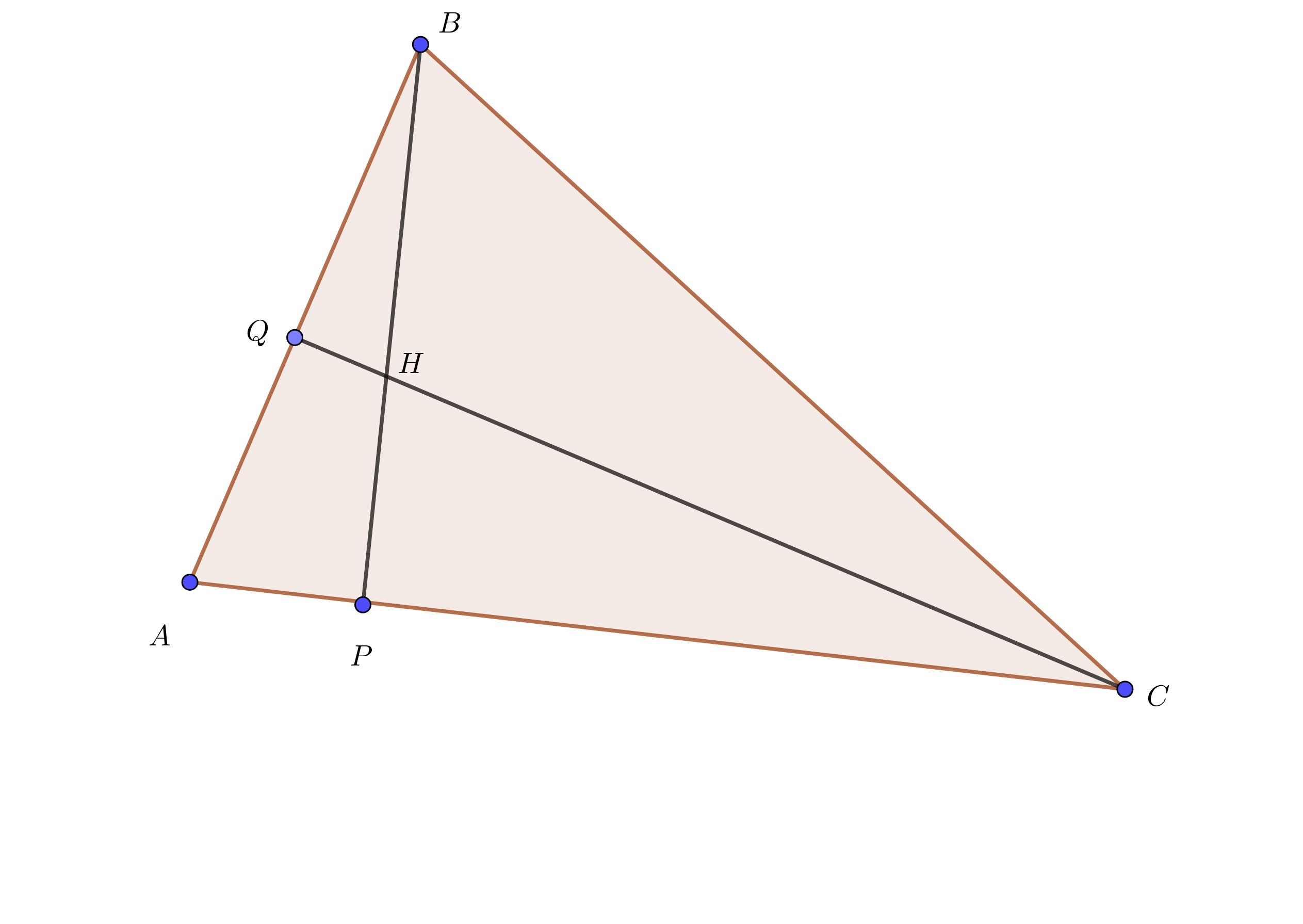
Высоты BP и CQ треугольника ABC пересекаются в точке H. Оказалось, что BH = AC. Найдите возможные значения угла ABC.

Answer 1

Треугольники BQH и ABP подобны. Также подобны треугольники AQC и ABP; Поэтому треугольники BQH и AQC подобны. При этом BH = AC, значит, эти треугольники равны. Отсюда BQ = QC и ∠ABC = 45°. Случаи с тупоугольным и прямоугольным треугольниками дают те же результаты