Предмет: Математика,
автор: svetochka19981
помогите решить диф. уравнение. даю 20 баллов. нужно второе
Приложения:
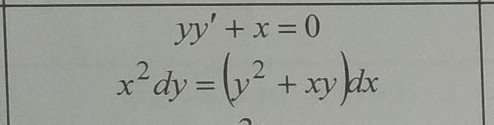
Ответы
Автор ответа:
2
Это уравнение можно переписать как - однородное уравнение, так как выполняется условие однородности.
Пусть , тогда дифференцируя(по формуле дифференцирования произведения двух функций):
и подставим в уравнение
Получили уравнение с разделяющимися переменными:
Обратная замена:
- ОБЩИЙ ИНТЕГРАЛ
Похожие вопросы
Предмет: Физика,
автор: pablenkolol
Предмет: Математика,
автор: lybaguziy03
Предмет: Биология,
автор: Pomogi1123
Предмет: Математика,
автор: Valentinch4
Предмет: Алгебра,
автор: badrudin2