Question

в треугольник с длиной основания a вписан квадрат, одна из сторон которого лежит на основании треугольника. Площадь квадрата оставляет 1/6 площади треугольника. Найти длину стороны квадрата. Варианты:
1) (корень из 6 -1)a/2 ; 2) (корень из 6+-1)a/2 ; 3) 6a/5 ; 4) (3+ корень из 6)a/6 ; 5) (3- корень из 6)a/6 ;

Решил самостоятельно, прикладываю решение:

Answer 1

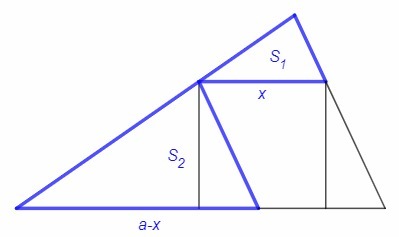
S - площадь треугольника, x - сторона квадрата.

Сторона квадрата, параллельная основанию треугольника, отсекает подобный треугольник с основанием x и площадью S1. Стороны квадрата, перпендикулярные основанию треугольника, отсекают треугольники, из которых складывается подобный треугольник с основанием a-x и площадью S2.

Площади подобных треугольников относятся как квадрат коэффициента подобия.

S1/S = x^2/a^2

S2/S = (a-x)^2/a^2

S1+S2 =5/6 S

(S1+S2)/S = (x^2 + (a-x)^2)/a^2 <=>

5/6 = (2x^2 -2ax +a^2)/a^2 <=>

12x^2 -12ax +6a^2 = 5a^2 <=>

x^2 -ax +a^2/12 =0 <=>

x1,2= (a+-√(a^2 -a^2/3))/2 =a(1+-√(2/3))/2 =a(3+-√6)/6

x<a: x=a(3-√6)/6