Предмет: Алгебра,
автор: valyabiryukov
Помогите решить задачу,
Приложения:
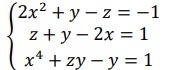
valyabiryukov:
xDF
Ответы
Автор ответа:
1
Сложим первое и второе уравнения этой системы:
Подставим полученное выражение для у во второе уравнение системы:
Получим систему уравнений:
или
или
Ответ: (-1;-2;1), (1;0;3)
Может 1:0:3? Там же 3, 1+1+1=3
В ответе
согласен. опечатка. дадут исправить - сделаю ))
Похожие вопросы
Предмет: Русский язык,
автор: nurtileksalmoorbekov
Предмет: Английский язык,
автор: ilnaznabiullin112233
Предмет: Другие предметы,
автор: SCUDEKILLER
Предмет: Физика,
автор: Астрид11