Предмет: Математика,
автор: oneluxpb3218
Сумма S существует и конечна. Найдите ее. Заранее спасибо)
Приложения:
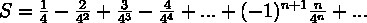
Ответы
Автор ответа:
1
решение на фото внизу
Ответ: 0,16
Приложения:

Автор ответа:
2
Вот еще забавный вариант:
Обозначим
G(x) = 1 - 1/x + 1/x^2 - 1/x^3 + 1/x^4 - ... =
= { |x| > 1 - бесконечная геом. прогрессия} = 1 / (1 + 1/x) = x / (x+1) = (x+1-1)/(x+1) = 1 - 1/(x+1)
G'(x) = 1/x^2 - 2/x^3 + 3/x^4 - 4/x^5 + ... = 1/(x+1)^2
Тогда
S = 1/4 - 2/4^2 + 3/4^3 - 4/4^4 + ... = 4 * (1/4^2 - 2/4^3 + 3/4^4 - 4/4^5 + ...) = 4 * G'(4) = 4/25 = 0.16
Похожие вопросы
Предмет: География,
автор: rmoskalev796
Предмет: Русский язык,
автор: ermolovamas
Предмет: Право,
автор: angelinakepsa16
Предмет: Литература,
автор: Klarissa1611
Предмет: Математика,
автор: 892737516791