Предмет: Алгебра,
автор: sargsyanroza2
Решите, пожалуйста, номер 4.
Приложения:
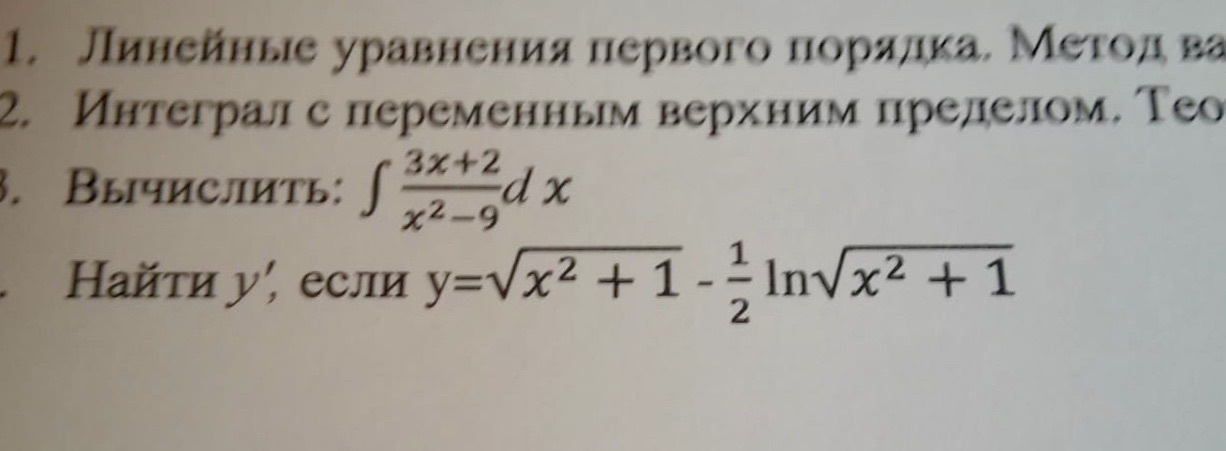
Ответы
Автор ответа:
1
найти , если
по правилу производной разности,
sargsyanroza2:
Огромное спасибо!
Похожие вопросы
Предмет: Биология,
автор: wwwwpppqqq
Предмет: Русский язык,
автор: velorihti
Предмет: Русский язык,
автор: Hanazuki3
Предмет: История,
автор: zewa1
Предмет: История,
автор: Кристина9403672