Предмет: Математика, автор: afroz1999azizop1zb2u

Проиводные y=(sin3x)^x

Ответы

Автор ответа: artalex74

$y=(\sin 3x)^x = e^{\ln (\sin 3x)^x} = e^{x \ln \sin 3x} \\<br />y'= e^{x \ln \sin 3x} \cdot (x \ln \sin 3x)' = (\sin 3x)^x \cdot ( \ln \sin 3x+\frac{3x \cos 3x}{\sin 3x} ) =\\ = (\sin 3x)^x \cdot ( \ln \sin 3x+3x ctg3x )$

Приложения:

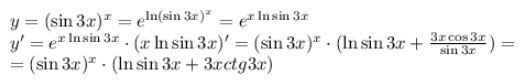
afroz1999azizop1zb2u: Надеюсь что правильно.

artalex74: а что остаётся? надеяться! )))

afroz1999azizop1zb2u: Если не правильно,то я знаю что сделать с тобой

artalex74: как я об этом узнаю?

afroz1999azizop1zb2u: 1 вопрос. Там у нас (sin3x)^x в конце тоже остался. Это как?

artalex74: Степенно-показательное выражение (sin3x)^x представляем через экспоненту е, т.к. ее производная известна. Причем (e^t)'=e^t·t' (производная сложной функции). Поэтому далее эта экспонента возвращается в исходный вид.

afroz1999azizop1zb2u: Ну теперь понял. Спасибо. Есть ВК

afroz1999azizop1zb2u: Если можно дайте пж?

Автор ответа: justcall

Можно также применить логарифмическое дифференцирование:

Приложения: