Предмет: Алгебра,
автор: octopus66177
Графически решить неравенство
Квадратный корень из 2 sin x <или= 1
Ответы
Автор ответа:
1
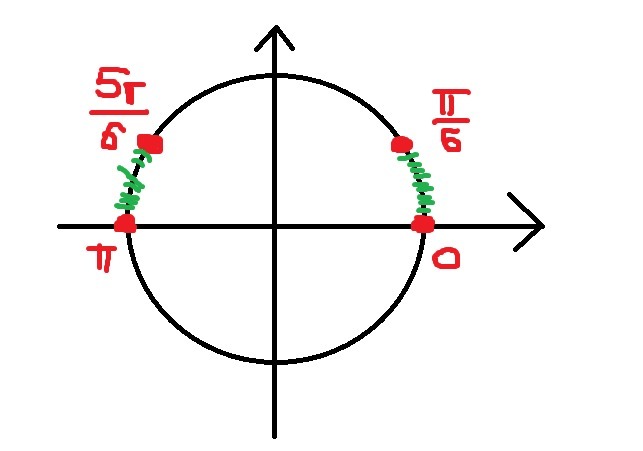
Ответ: x ∈ [π; 5π/6] ∪ [π/6; 0] + 2πn, n ∈ Z
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: catherine9580
Предмет: Английский язык,
автор: rohaninadasha2007
Предмет: Английский язык,
автор: nazardubinskyy28
Предмет: Биология,
автор: Машутка66
Предмет: Химия,
автор: лейла1234567890