Предмет: Математика,
автор: gparczaxashvili
вычислить площадь фигуры ограниченной линиями y=x^2 y=2x+8
Ответы
Автор ответа:
6
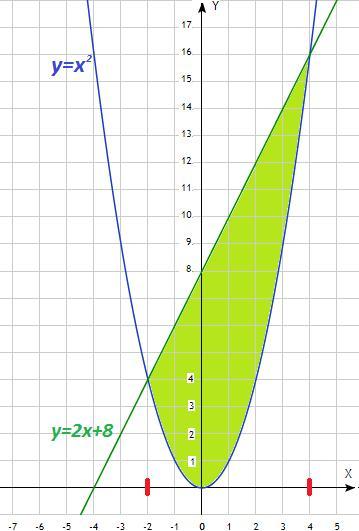
y = x² - квадратичная функция, график - парабола, ветви направлены вверх.
y = 2x + 8 - линейная функция, график - прямая линия.
Точки пересечения графиков :
x² = 2x + 8
x² - 2x - 8 = 0
(x + 2)(x - 4) = 0
x₁ = -2; x₂ = 4 - пределы интегрирования
Площадь фигуры ограничена сверху прямой линией y=2x+8, снизу параболой y=x² ( см. рисунок).
Ответ : 36
Приложения:
Автор ответа:
2
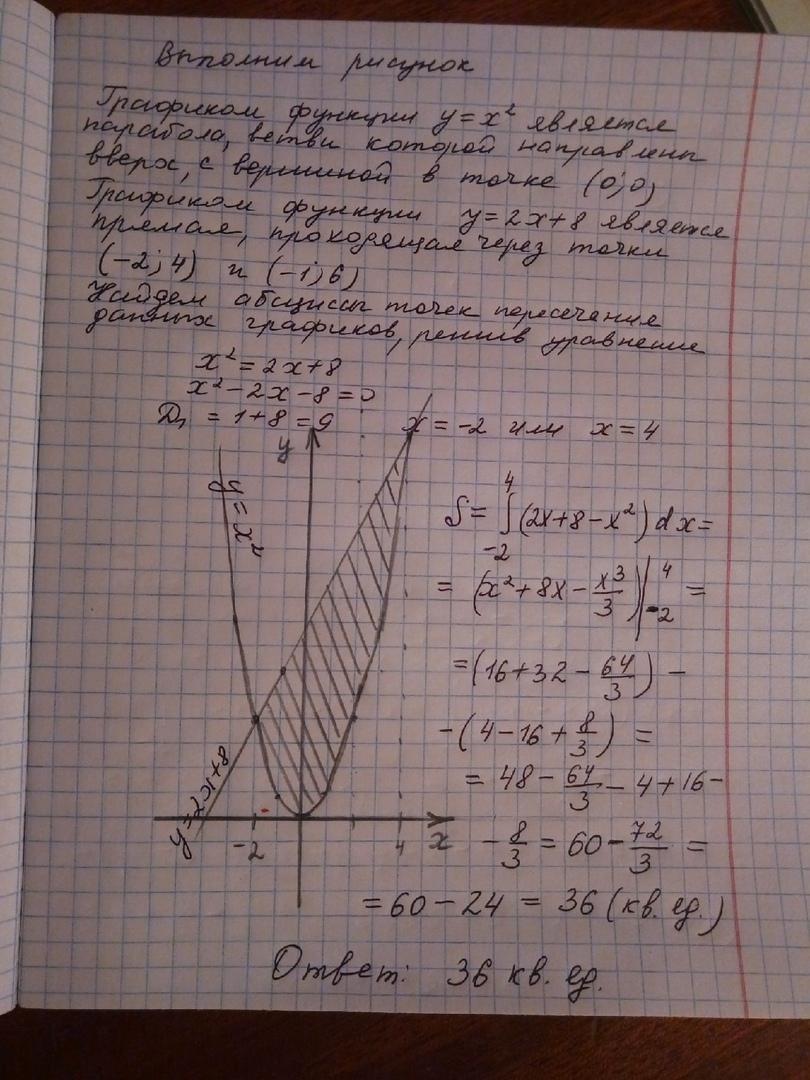
Ответ:
решение представлено на фото
Пошаговое объяснение:
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: andrejlokoti567
Предмет: История,
автор: Аноним
Предмет: Қазақ тiлi,
автор: makokrasavets
Предмет: Математика,
автор: Anna12444