Question

Докажите, что отрезок соединяющий середины противоположных сторон выпуклого четырехугольника меньше полусуммы его диагоналей

Answer 1

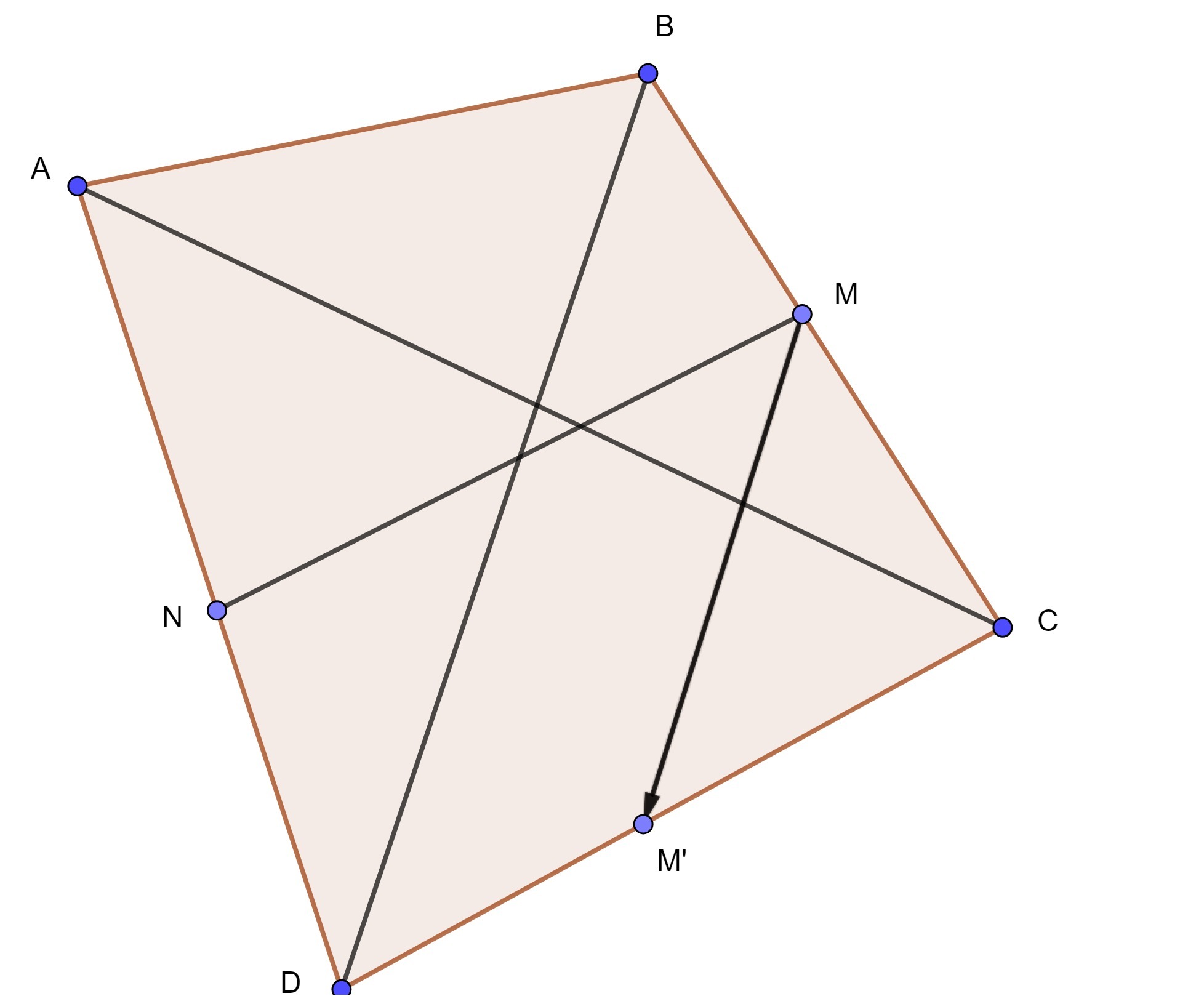
Рассмотрим четырехугольник ABCD; Пусть в нем диагональ AC зафиксирована, то есть имеет постоянную длину. Минимальная полусумма диагоналей получается тогда, когда вторая диагональ имеет нулевую длину. В таком случае точка B переходит в точку D. Рассмотрим отрезок MN - тот, что соединяет середины сторон BC и AD. Он сместился в точку M', причем MN ║ BD, поскольку B сместилась в D. Точка N осталась на прежнем месте. Получили треугольник ACD в котором M'N - средняя линия. Поэтому $M'N=\frac{1}{2}AC$, но мы рассматриваем четырехугольник, никакие две вершины которого не лежат друг на друге. Значит, в остальных случаях $\frac{AC+BD}{2}>MN$

Answer 2

решение смотри в файле.