Question

Кто знает как решить????

Answer 1

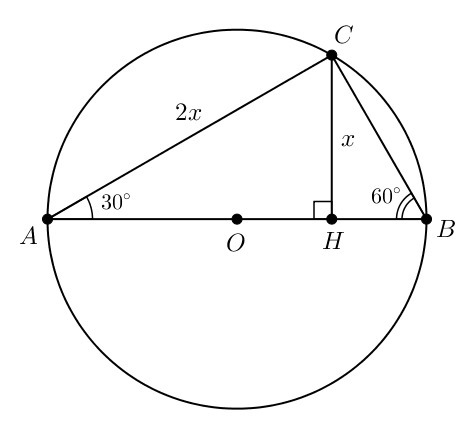
Обозначим CH как x, а AC — как 2x (см. рисунок). Очевидно, Δ ACH — прямоугольный треугольник, AC — гипотенуза. Сначала найдём угол A по теореме синусов:

$\displaystyle \frac{2x}{\sin 90^{\circ}}=\frac{x}{\sin \angle A}}\\ \frac{1}{\sin \angle A}=2 \\ \sin \angle A= \frac{1}{2}; \\ \angle A= 30^{\circ}$

(При условии, что 0°<∠A<90°, поэтому значение ∠A=150° не подходит.)

Кстати, угол можно вычислить быстрее, если вспомнить, что когда катет в два раза меньше гипотенузы, то противолежащий к нему угол равен 30°.

Угол ∠ACB равен 90°, поскольку опирается на диаметр окружности. Поэтому ∠ABC = 180°–(90°+30°)=180°–120°=60°.

Answer 2

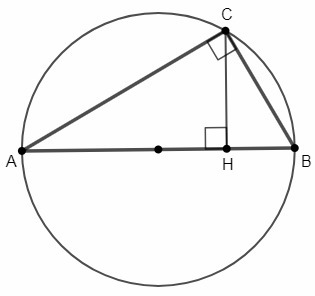
Если катет равен половине гипотенузы, он лежит против угла 30°.

△ACH - прямоугольный (CH⊥AB), CH=AC/2 => ∠A=30°

Вписанный угол ACB - прямой, так как опирается на диаметр.

∠B= 90°-30° =60°