Question

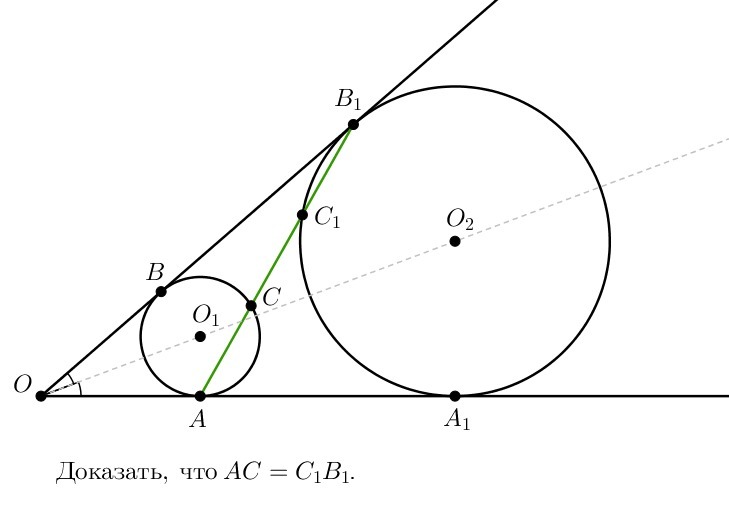
В угол вписаны две окружности. Точки A и B — точки касания первой окружности, точки $A_1$ и $B_1$ — точки касания второй окружности (см. рисунок). Отрезок $AB_1$ пересекает эти окружности в точках $C$ и $C_1$. Докажите, что $AC=B_1C_1$.

С полным доказательством, пожалуйста.

Answer 1

Есть теорема-

Если из внешней точки к окружности проведены касательная и секущая, то квадрат отрезка касательной от данной точки до точки касания равен произведению длин отрезков секущей от данной точки до точек её пересечения с окружностью.

По ней AA1^2=C1B1*AC1 -для большой окружности

и BB1^2=B1C*AC-для малой

Так как BB1=AA1-приравниваю и правые части равенств

С1B1*AC1=B1C*AC

C1B1*(AC+CC1)=(CC1+C1B1)*AC

C1B1*AC+C1B1*CC1=CC1*AC+C1B1*AC

следует С1B1=AC