Предмет: Математика,
автор: 0vvl
При каком значении a система неравенств имеет единственное решение
Приложения:
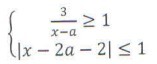
Ответы
Автор ответа:
2
первое выражение ≥1, второе ≤ 1.
Эта система будет иметь решение, только если оба этих выражения будут РАВНЫ 1 !
Выражаем из первого х:
и подставляем во второе:
Остается проверить, при каком из полученных параметров будет одно решение:
1) a=0
Не удовлетворяет условию!
2) a=2
ОТВЕТ: a=2
0vvl:
В конце опечатка, не "51", а "5")
да,да
там должно быть от 5 до 7
Похожие вопросы
Предмет: Математика,
автор: ldubincova
Предмет: Русский язык,
автор: karnavalvala078
Предмет: Русский язык,
автор: janibekov2012
Предмет: Математика,
автор: соник54