Предмет: Математика,
автор: natablumekozl
Как решить дефференциальньное уравнение?
Приложения:

Ответы
Автор ответа:
0
Примем:
Ответ:
Приложения:
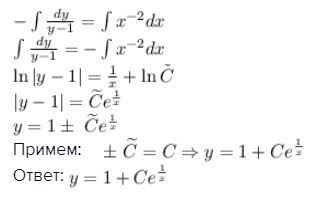
Похожие вопросы
Предмет: Математика,
автор: donskovnikolaj6
Предмет: Английский язык,
автор: alina106232
Предмет: Русский язык,
автор: zahsasa108
Предмет: Математика,
автор: помогитепожалуйста68
Предмет: Литература,
автор: ekaterinkass