Предмет: Алгебра,
автор: Sundelly
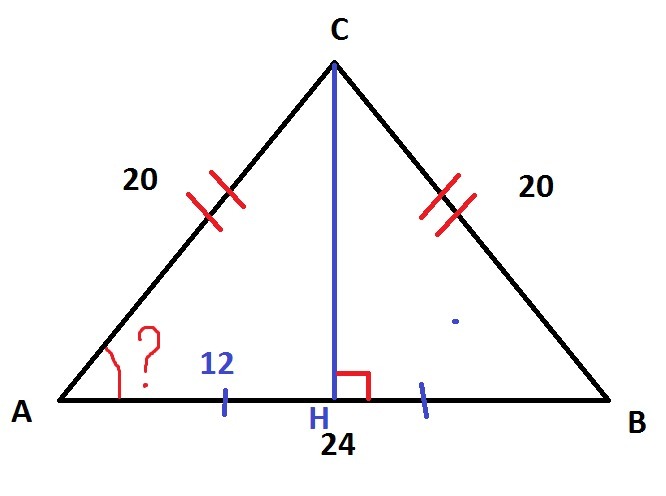
В треугольнике ABC, AC=BC=20 , AB=24. найдите cos A
Ответы
Автор ответа:
1
1 способ.
Проведем высоту СН. Так как треугольник равнобедренный (AC=BC), значит СН также и медиана и высота. То есть АН=НВ=24/2=12
В прямоугольном ΔАСН:
2 способ
По теореме косинусов:
Приложения:
Похожие вопросы
Предмет: Математика,
автор: hr2h2ftmw8
Предмет: Математика,
автор: sabrinadadasova8
Предмет: Английский язык,
автор: albinabofabaeva
Предмет: Математика,
автор: 93939393
Предмет: Математика,
автор: Kakjgjngf