Предмет: Алгебра,
автор: arol01pattcy
Помогите решить ЕГЭ
ПРОШУ ВАС СРОЧНО НУЖНА
ЗАВТРА ЕГЭ!!!
МНЕ РЕШЕНИЕ НУЖНО!
Приложения:
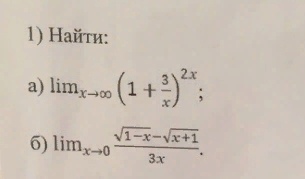
Ответы
Автор ответа:
8
а) Неопределенность: . Значит будем использовать второй замечательный предел.
б) Умножим числитель и знаменатель дроби на , имеем:
Похожие вопросы
Предмет: Алгебра,
автор: galymkojsybaev964
Предмет: Қазақ тiлi,
автор: erasyltaigulov000
Предмет: Українська література,
автор: vysockyislava
Предмет: Физика,
автор: RR8Dale