Предмет: Алгебра,
автор: Mariaglu2
x²-3|x|+2≤0 розвязати нерівність ....................
Ответы
Автор ответа:
4
решение на фотографии
Приложения:
Автор ответа:
1
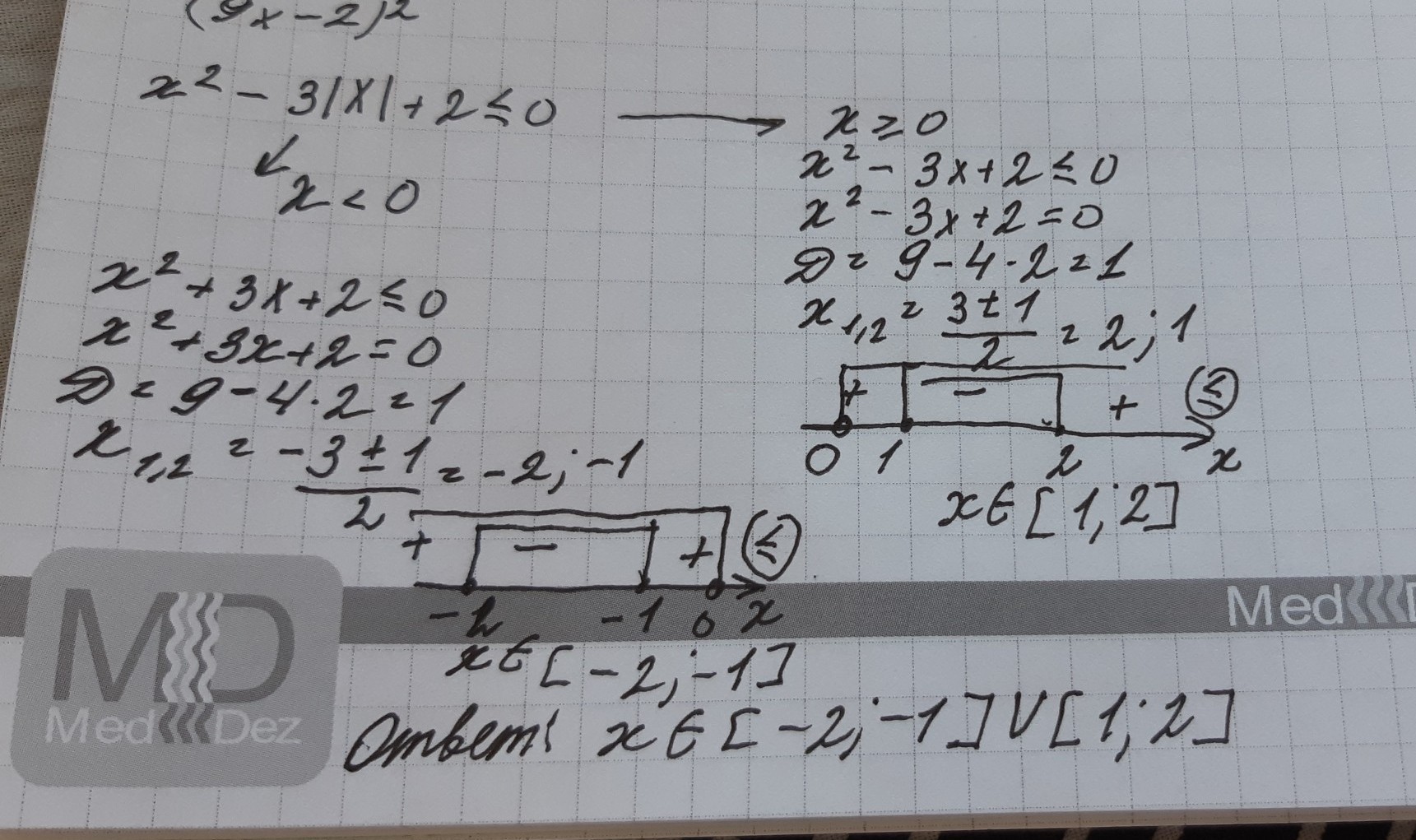
x^2-3|x|+2<=0
1. X>=0, y=x^2-3x+2
x^2-3x+2=0
D=9-4-2=1
x1=(3-1)/2=1; x2=(3+1)/2=2
+ - +
---------.--------.------------------>
1 2
x>=0, x∈[1;2]
2.x<0, x^2-3*(-x)+2<=0
x^2+3x+2=0
D=9-4*2=1
x1=(-3+1)/2=-1; x2=(-3-1)/2=-2
+ - +
---------.-------------------.---------------->
-2 -1
x<0 x∈[-2;-1]
otvet x∈[-2;-1];[1;2].
1. X>=0, y=x^2-3x+2
x^2-3x+2=0
D=9-4-2=1
x1=(3-1)/2=1; x2=(3+1)/2=2
+ - +
---------.--------.------------------>
1 2
x>=0, x∈[1;2]
2.x<0, x^2-3*(-x)+2<=0
x^2+3x+2=0
D=9-4*2=1
x1=(-3+1)/2=-1; x2=(-3-1)/2=-2
+ - +
---------.-------------------.---------------->
-2 -1
x<0 x∈[-2;-1]
otvet x∈[-2;-1];[1;2].
Приложения:
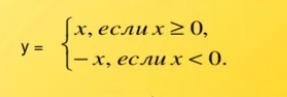
InvisorTech:
У вас допущена ошибка в решении. Из-за этого ответ неверен.
От Вас требовалось при решении найти объединение двух случаев, где x больше или равно нулю и x строго меньше нуля.
Похожие вопросы
Предмет: Українська література,
автор: raufov405
Предмет: Биология,
автор: didarzeten
Предмет: Другие предметы,
автор: Аноним
Предмет: Химия,
автор: Aшлy
Предмет: Алгебра,
автор: Неуловимыйтип