Предмет: Алгебра,
автор: Marino4ka16
Пожалуйста! Составьте уравнение нормали к кривой у=f(х) в точке х=х0. В ответе укажите ординату точки с абсциссой х1=1, лежащей на нормали.
Приложения:
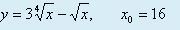
Ответы
Автор ответа:
1
Делаем производную
уравнение касательной:
подставляем
Или же во вменяемом виде:
Итого, вектор нормали нашей касательной есть (1, 32). Вектор есть, строим прямую по вектору и точке.
Или же
Похожие вопросы
Предмет: Русский язык,
автор: gulnazik1985
Предмет: Қазақ тiлi,
автор: mutanakbota824
Предмет: Химия,
автор: mschemiakin
Предмет: Физика,
автор: Astralina