Question

Помогите решить уравнение

Answer 1

$\frac{x}{(x+1)*4^x-1} =\frac{8}{5-3*2^x} \\ \\ x(5-3*2^x)=8(x+1)*4^x-8\\ \\ 5x-3x*2^x=(8x+8)*2^{2x}-8\\ \\ (8x+8)*2^{2x}+3x*2^x-(5x+8)=0\\ \\ D=9x^2+4(8x+8)(5x+8)=9x^2+4(40x^2+40x+64x+64)=\\ \\ 97x^2+160x^2+416x+256=169x^2+416x+256=(13x+16)^2\\ \\ 1)2^x=\frac{-3x-13x-16}{16x+16} =-1$

нет корней

$2)2^x=\frac{-3x+13x+16}{16x+16} =\frac{5x+8}{8x+8} \\ \\ \left \{ {{y=2^x} \atop {y=\frac{5x+8}{8x+8}}} \right.$

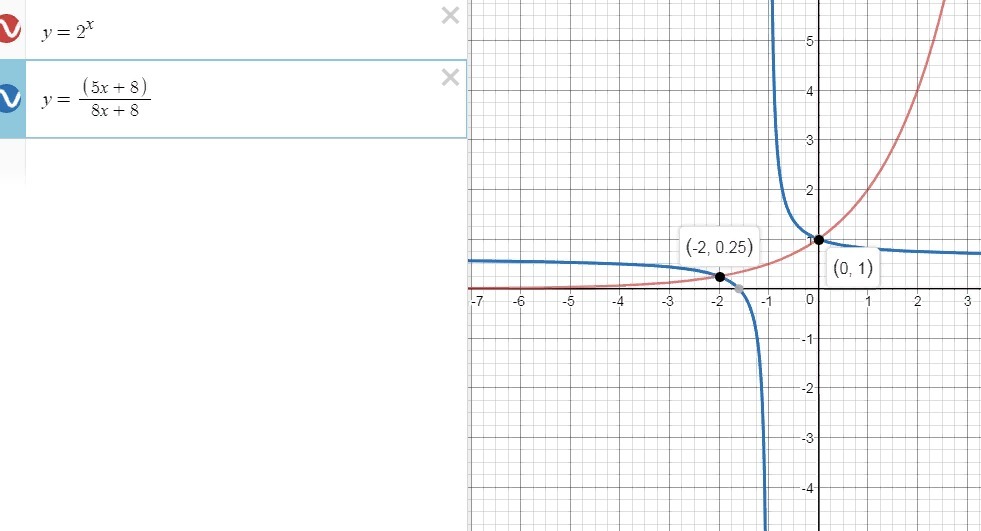
решаем графически

x₁=0

подставим в исходное уравнение, в знаменателе получаем 0,⇒ не подходит

х₂=-2

подставим в исходное уравнение

равенство выполняется,⇒ х=-2 является корнем уравнения

$\frac{-2}{(-2+1)*4^{-2}-1} =\frac{-2}{-\frac{1}{16}-1} =\frac{32}{17} \\ \\ \frac{8}{5-3*2^{-2}} =\frac{8}{5-\frac{3}{4}} =\frac{32}{17} \\ \\ OTVET:x=-2$