Предмет: Алгебра,
автор: AlexFil31
Исследовать на абсолютную и условную сходимость ряд:
Приложения:
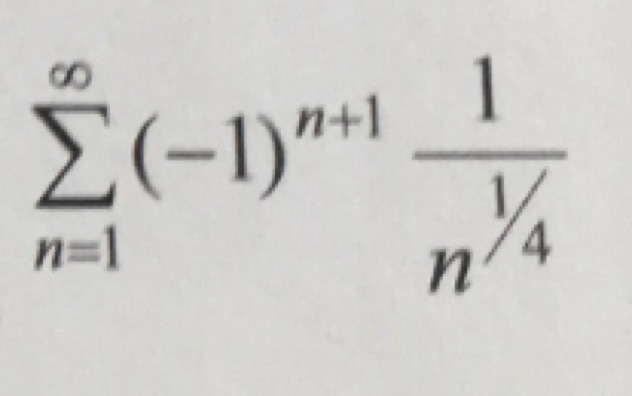
Ответы
Автор ответа:
1
Ряд сходится условно, т.к. все условия признака Лейбница выполняются, а ряд составленный из абсолютных величин является обобщённо гармоническим расходящимся рядом.
Автор ответа:
0
1. Первое условие признака Лейбница выполняется, т.е. каждый последующий член ряда меньше предыдущего
По признаку Лейбница ряд сходится.
Проверим теперь на абсолютность сходимости ряда, взяв ряд по модулю
И этот ряд расходится, следовательно данный ряд сходится условно.
Похожие вопросы
Предмет: Русский язык,
автор: natalikis2000
Предмет: Геометрия,
автор: sllallalalwlwl
Предмет: Русский язык,
автор: vihihs1987
Предмет: Биология,
автор: Toperумный
Предмет: Математика,
автор: Джульетта1111