Question

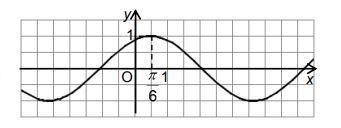
Дан график функции $f(x)=cos(x-\frac{\pi}{6})$
1) Назовите два значения аргумента x, при котором значение функции равно 1.
2) Назовите нули функции в интервале $(-\pi ;\pi )$.
3) Назовите все значения аргумента х, при котором функция положительна.
4) Нарисуйте на данной координатной прямой график функции $g(x)=-cos(x-\frac{\pi}{6})$

Answer 1

1) π/6; π/6 + 2π

2) -π/3; 2π/3

3) (-π/3 + 2πk; 2π/3 + 2πk) k∈Z

4) график будет таким же, только как отражение относительно Ох, т.е. в π/6 значение будет -1, нули будут в тех же точках