Предмет: Математика,
автор: dmitrich991
Общим решением дифференциального уравнения cos xdx + e^-2y dy= 0 является ....
(См. Фото)
Приложения:
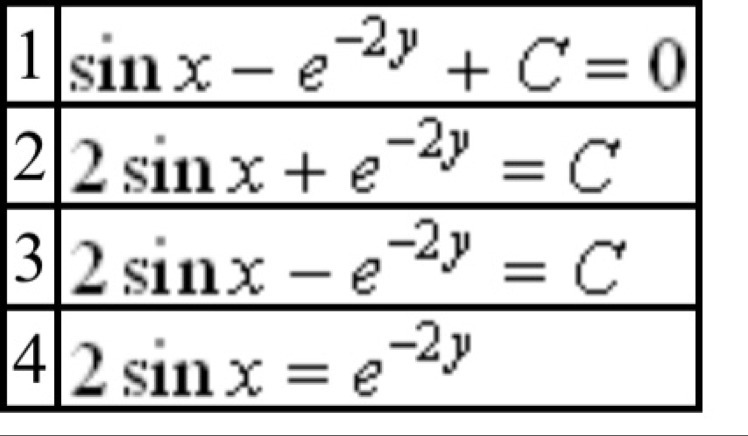
Ответы
Автор ответа:
1
Ответ 3
Похожие вопросы
Предмет: Другие предметы,
автор: xxxelekto123
Предмет: Математика,
автор: xosTUwU11
Предмет: Қазақ тiлi,
автор: aishaazn09
Предмет: Математика,
автор: lavrenkova19991
Предмет: Геометрия,
автор: Keksik322