Предмет: Алгебра,
автор: nhito728
Производные
1. ((sinx+cosx)²)'
2.(1+tg²x/1+ctg²x)'
3.(lnsinx)'
Ответы
Автор ответа:
0
1) (sin x+cos x)²= 1 + sin2x ⇒ (1 + sin2x)' = 2cos2x ⇒ ((sin x+cos x)²)' = 2cos2x
2)
⇒ ⇒
3)
Приложения:
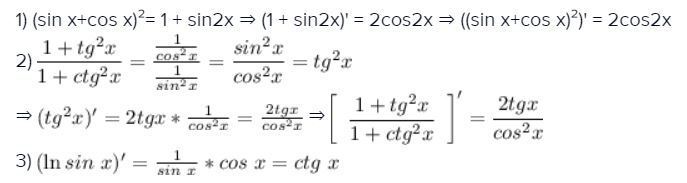
Автор ответа:
1
решение смотри на фотографии
Приложения:

Похожие вопросы
Предмет: История,
автор: rostovcevamasa902
Предмет: Русский язык,
автор: dyhwbsmk
Предмет: Математика,
автор: Аноним
Предмет: Математика,
автор: lavrenkova19991
Предмет: История,
автор: easyyashkaaa