Предмет: Математика,
автор: daniya136
Помогите с решением?))))
Приложения:
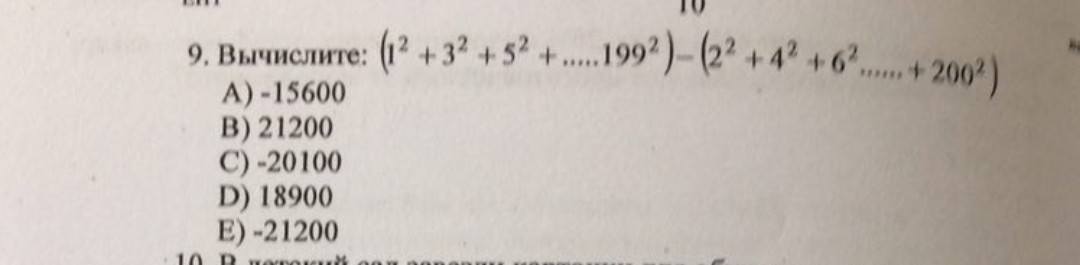
Ответы
Автор ответа:
0
1²+3²+5²+...n²=1/6*n*(n+1)*(n+2)
199*200*201/6 = 1333300
200*201*202/6 = 1353400
1333300–1353400 = –20100
Или:
1²+3²+5²+...n²=1/6*((n+1)³–(n+1))
(200³–200)/6 = 1333300
(201³–201)/6 = 1353400
1333300–1353400 = –20100
199*200*201/6 = 1333300
200*201*202/6 = 1353400
1333300–1353400 = –20100
Или:
1²+3²+5²+...n²=1/6*((n+1)³–(n+1))
(200³–200)/6 = 1333300
(201³–201)/6 = 1353400
1333300–1353400 = –20100
daniya136:
я не поняла почему вы приравняли 1^2+2^2=.1/6..
Там дальше выражение
Это формулы, чтобы найти сумму квадратов нечетного или четного ряда чисел. Сделано по действиям: отдельно посчитаны первая и вторая части выражения, потом разность. Две равнозначные формулы - два варианта решения.
1²+3²+5²+...n²=1/6*n*(n+1)*(n+2); 2²+4²+6²+...n²=1/6*n*(n+1)*(n+2). n - это последнее число в ряду.
Аааа, спасибо большое
Пожалуйста.
Похожие вопросы
Предмет: Алгебра,
автор: firpozzi01
Предмет: Математика,
автор: Antile
Предмет: Алгебра,
автор: michiepetrovabts
Предмет: Математика,
автор: Элисон111