Question

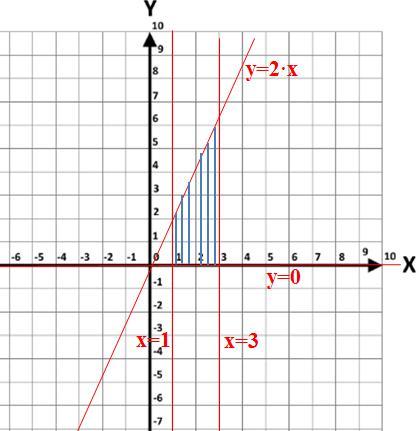
вычислите площадь фигуры,ограниченной линиями у=2х,у=0,х=1,х=3

Answer 1

Ответ:

12 (кв. единиц)

Объяснение:

Рисуем фигуру (см. рисунок) с помощью заданных прямых:

1) точка пересечения прямых y=2·x и y=0:

2·x=0 ⇔ x=0 ⇒ y=2·0=0 ⇒ (0; 0)

2) точка пересечения прямых y=0 и x=1: (1; 0)

3) точка пересечения прямых y=0 и x=3: (3; 0)

4) точка пересечения прямых y=2·x и x=1:

y=2·1=2 ⇒ (1; 2)

5) точка пересечения прямых y=2·x и x=3:

y=2·3=6 ⇒ (3; 6).

Получается прямоугольная трапеция с основаниями a=6 и b=2, высотой h=3-1=2.

Тогда площадь фигуры (трапеции) равна

$\displaystyle \tt S=\frac{a+b}{2} \cdot h = \frac{6+2}{2} \cdot 2 = 12.$