Предмет: Геометрия,
автор: bryukhanovaekat
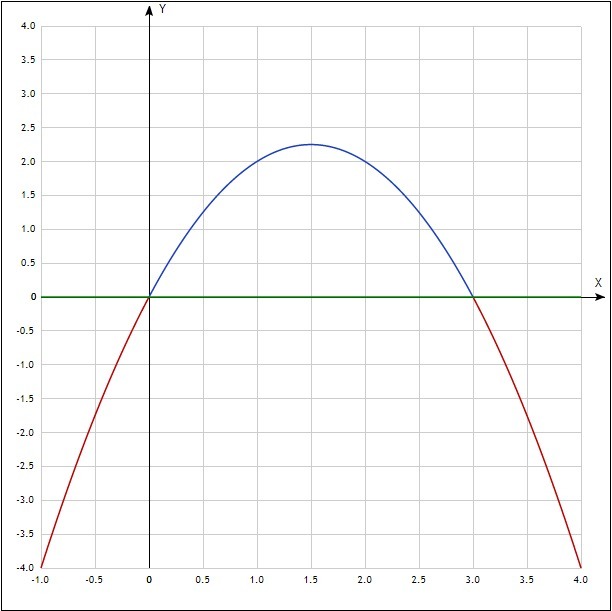
вычислите площадь криволинейной трапеции ограниченной линиями f(x) =-x²+3x, y=0
Ответы
Автор ответа:
0
f(x) = x(- x + 3)
точки пересечения с прямой y = 0
x₁ = 0
x₂ = 3
---
Площадь фигуры между параболой и осью Ох

точки пересечения с прямой y = 0
x₁ = 0
x₂ = 3
---
Площадь фигуры между параболой и осью Ох
Приложения:
Похожие вопросы
Предмет: Музыка,
автор: Alekjej
Предмет: Алгебра,
автор: weunly
Предмет: Қазақ тiлi,
автор: adilimangaliev473
Предмет: Литература,
автор: Екатерина9865