Предмет: Математика,
автор: danilkornilov
помогите
пожалуйста решить
Приложения:
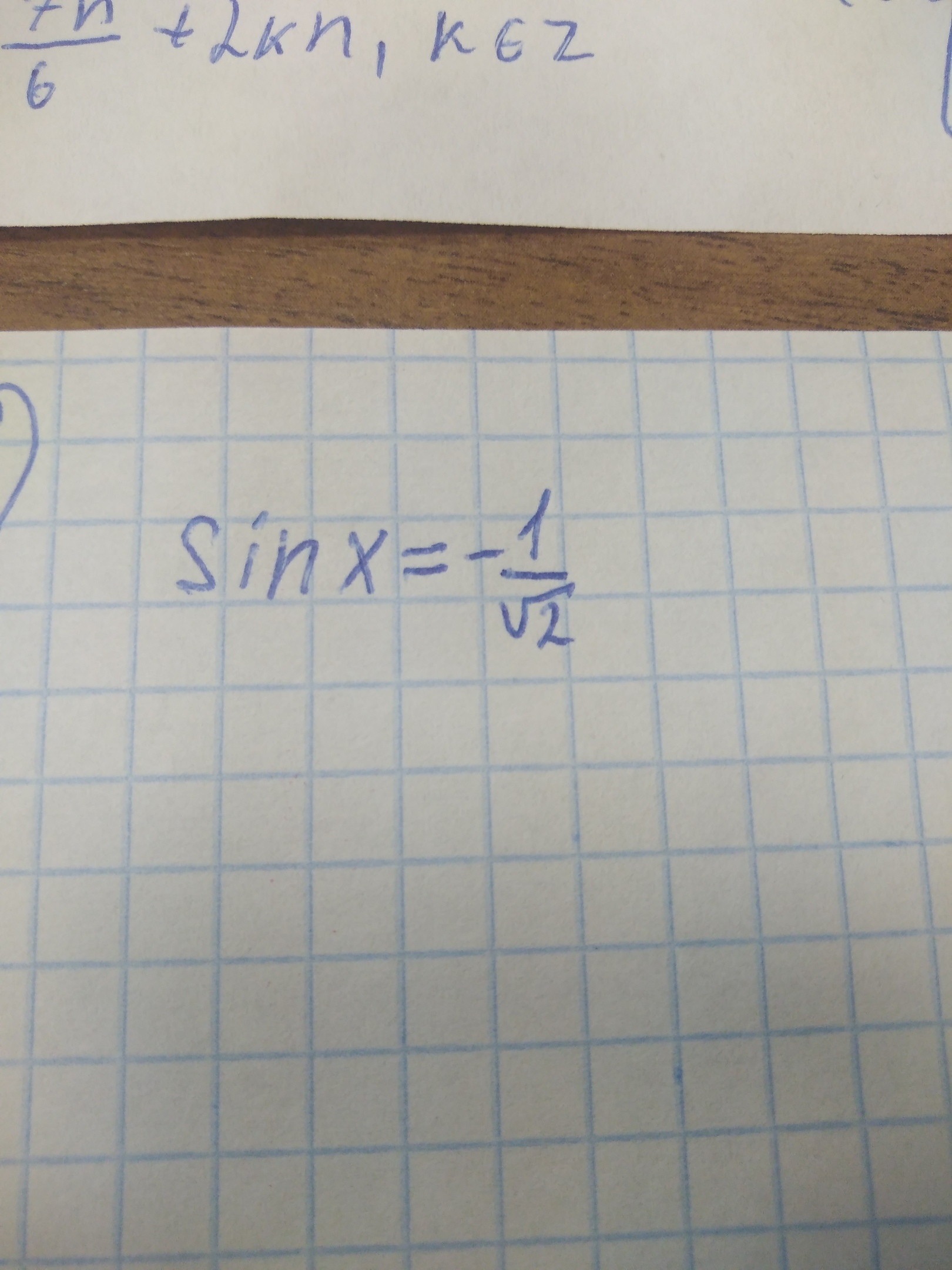
Ответы
Автор ответа:
0
Каждое действие подчеркнуто линией.
___________________________________
Объяснения:
1) Избавляемся от иррациональности в знаменателе, т.е. умножить числитель и знаменатель на √2. Любое выражение, умноженное на1, не изменяется. При умножении квадратного корня из некоторого выражения на себя результатом является данное выражение.
2), 3) Рассмотрим все возможные случаи. Поскольку sin (t)=sin (π-1), уравнение имеет два решения. Чтобы убрать х, нужно использовать обратную тригонометрическую функцию. Чтобы убрать π-х, надо использовать обратную тригонометрическую функцию.
4) Использую таблицу значений тригонометрических функций или единичную окружность, -√2/2⇒-π/4
5) Поскольку sin (х) и sin (π-х) являются периодическими функциями, нужно добавить период 2kπ, k∈Z для нахождения всех решений.
6) Дальше находим наименьший положительный угол и решаем уравнение.
7) Т.к. k∈Z⇒-2kπ=2kπ
_______________________
Розовая линия:
у=-1/√2
Зеленая линяя:
у=sinx
Корень (kπ, 0), k∈Z
Область определения х∈R
Максимум (π/2 +2kπ, 1) k∈Z
Минимум (3π/2 + 2kπ, -1) k∈Z
Пересечение с осью у (0,0)
___________________________________
Объяснения:
1) Избавляемся от иррациональности в знаменателе, т.е. умножить числитель и знаменатель на √2. Любое выражение, умноженное на1, не изменяется. При умножении квадратного корня из некоторого выражения на себя результатом является данное выражение.
2), 3) Рассмотрим все возможные случаи. Поскольку sin (t)=sin (π-1), уравнение имеет два решения. Чтобы убрать х, нужно использовать обратную тригонометрическую функцию. Чтобы убрать π-х, надо использовать обратную тригонометрическую функцию.
4) Использую таблицу значений тригонометрических функций или единичную окружность, -√2/2⇒-π/4
5) Поскольку sin (х) и sin (π-х) являются периодическими функциями, нужно добавить период 2kπ, k∈Z для нахождения всех решений.
6) Дальше находим наименьший положительный угол и решаем уравнение.
7) Т.к. k∈Z⇒-2kπ=2kπ
_______________________
Розовая линия:
у=-1/√2
Зеленая линяя:
у=sinx
Корень (kπ, 0), k∈Z
Область определения х∈R
Максимум (π/2 +2kπ, 1) k∈Z
Минимум (3π/2 + 2kπ, -1) k∈Z
Пересечение с осью у (0,0)
Приложения:

Похожие вопросы
Предмет: Английский язык,
автор: as5088054
Предмет: Математика,
автор: marvanovaanita
Предмет: Химия,
автор: LiMon4ki
Предмет: Математика,
автор: гуля214