Предмет: Алгебра,
автор: AlinochkaAngelok
Решите пожалуйста 1 и 3
Приложения:

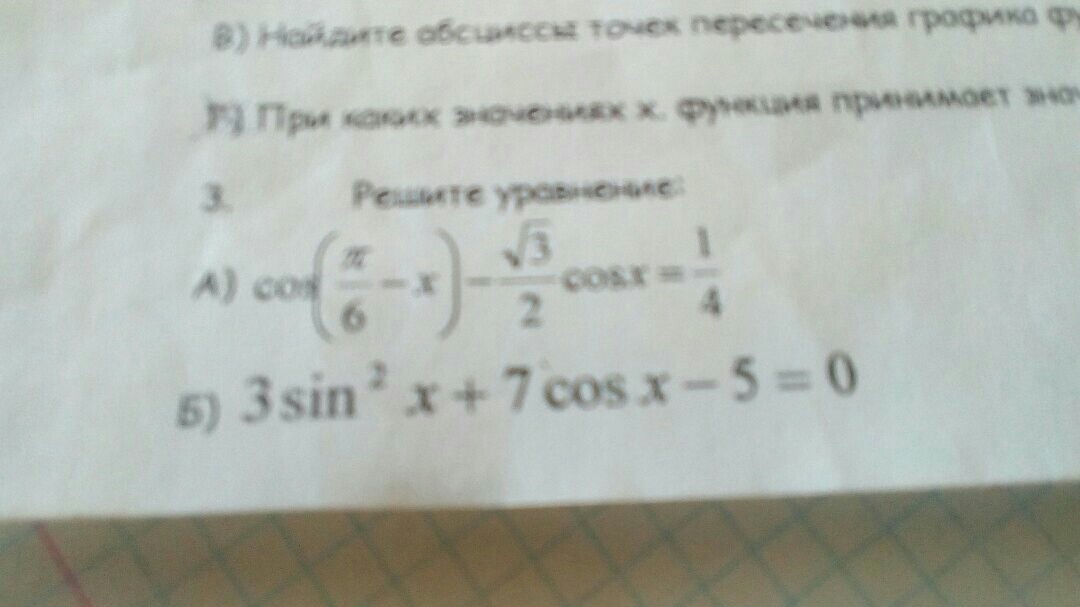
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: Алгебра,
автор: lavenkoyana08
Предмет: Математика,
автор: eashatovna
Предмет: Математика,
автор: Аноним
Предмет: Математика,
автор: Anna70720031
Предмет: Математика,
автор: Kadyrin