Question

Трапеция KLMN с основаниями KN и LM вписана окружность , центр которой лежит на основании KN.Диогональ KM трапеции равна 4 см , а боковая сторона Kl равна 3 с . Определите длину основания LM. Строно !!

Answer 1

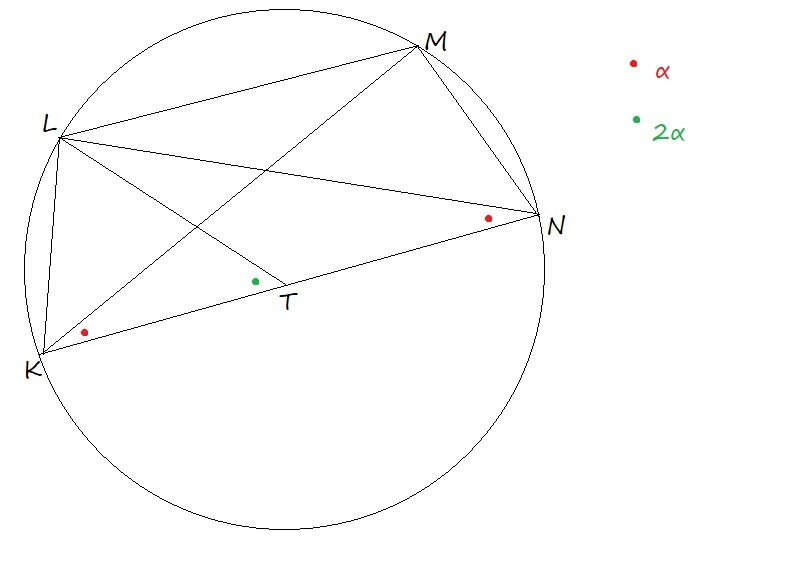
Во-первых, трапеция которая вписана в окружность является равнобедренной, поскольку: 1) сумма противоположных углов четырехугольника равна 180°; 2) сумма односторонних углов трапеции равна 180°; Значит углы при основании равны.

Пусть радиус окружности равен R; При этом TK = TN = R; По теореме синусов: $KL=2R \sin \alpha =3$
Поскольку LT = KT как радиусы, треугольник LTK - равнобедренный и ∠KLT = ∠LKT = (180°-2α)/2 = 90-α; По теореме синусов: $LN = 2R \sin(90^{0}- \alpha )= 2R\cos \alpha =4$; С одной стороны $2R= \frac{3}{\sin \alpha }$, с другой $2R = \frac{4}{\cos \alpha }$, откуда $\sin \alpha =0,6$; 2R = 5; Опустим перпендикуляры на основание с точек L и M; Тогда $LM = KN-2KL\sin \alpha =5-2*3*0,6=1,4$