Предмет: Математика,
автор: МатематическийМозг
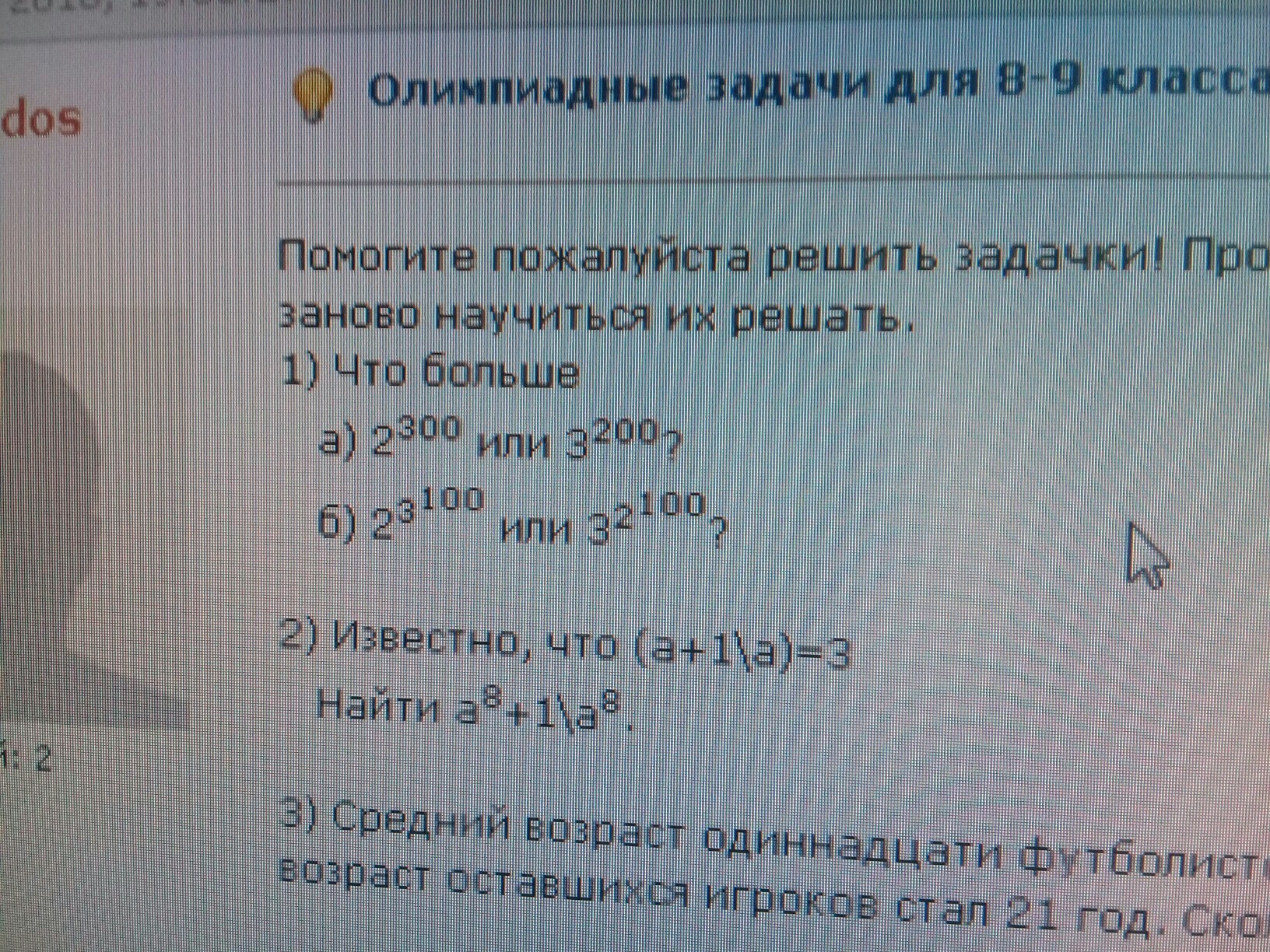
решите только 1. б)
Приложения:
Ответы
Автор ответа:
1
смотри решение во вложении
Приложения:
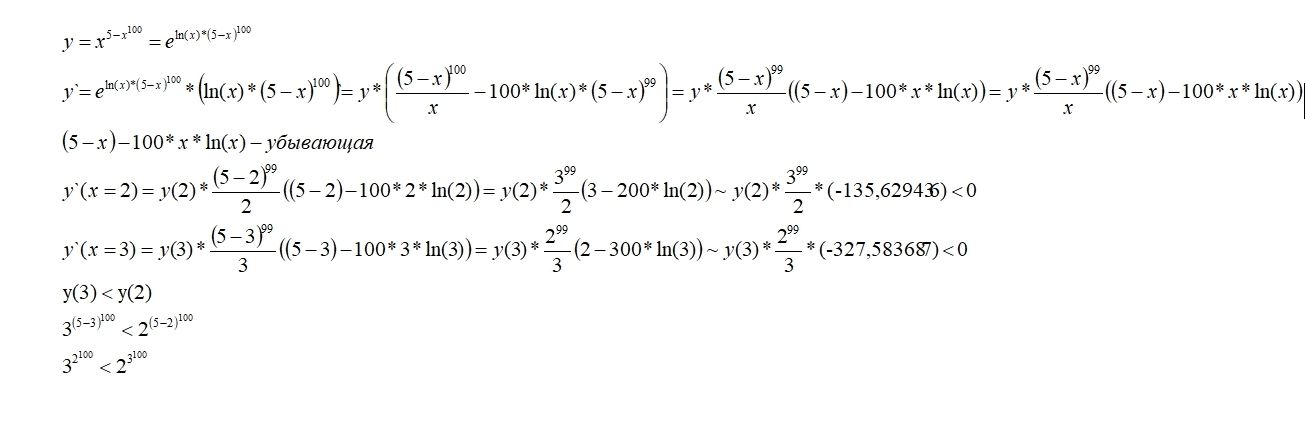
Автор ответа:
1
1.а) 2³⁰⁰ = (2³)¹⁰⁰ = 8¹⁰⁰
3²⁰⁰ = (3²)¹⁰⁰ = 9¹⁰⁰
1 < 8 < 9 ⇒ 8¹⁰⁰ < 9¹⁰⁰ ⇒ 2³⁰⁰ < 3²⁰⁰
---------------------------------------------------------------
1. б)
I способ

a₂ < a₃ < a₄ ... ⇒
Скорость роста выше скорости роста
выше скорости роста  при n ↑
при n ↑
⇒
II способ.
 ⇔ так как (2>1)
⇔ так как (2>1)
 ⇔
⇔
 | : 2¹⁰⁰>0
| : 2¹⁰⁰>0
1,5¹⁰⁰ |?| log₂3 ⇔
1,5¹⁰⁰ |?| log₂ (4*3/4)
1,5¹⁰⁰ |?| log₂4 + log₂(3/4)
1,5¹⁰⁰ |?| 2 + log₂(3/4)
(2>1) и (3/4)<1 ⇒ log₂(3/4)<log₂1<0 ⇒
2+log₂(3/4) < 2
1,5¹⁰⁰ = (1,5²)⁵⁰ = 2,25⁵⁰
2,25ˣ - возрастающая, так как 2,25 > 1 ⇒
1,5¹⁰⁰ = 2,25⁵⁰ > 2,25¹ > 2 ⇒
1,5¹⁰⁰ > 2 + log₂(3/4) ⇔

3²⁰⁰ = (3²)¹⁰⁰ = 9¹⁰⁰
1 < 8 < 9 ⇒ 8¹⁰⁰ < 9¹⁰⁰ ⇒ 2³⁰⁰ < 3²⁰⁰
---------------------------------------------------------------
1. б)
I способ
a₂ < a₃ < a₄ ... ⇒
Скорость роста
⇒
II способ.
1,5¹⁰⁰ |?| log₂3 ⇔
1,5¹⁰⁰ |?| log₂ (4*3/4)
1,5¹⁰⁰ |?| log₂4 + log₂(3/4)
1,5¹⁰⁰ |?| 2 + log₂(3/4)
(2>1) и (3/4)<1 ⇒ log₂(3/4)<log₂1<0 ⇒
2+log₂(3/4) < 2
1,5¹⁰⁰ = (1,5²)⁵⁰ = 2,25⁵⁰
2,25ˣ - возрастающая, так как 2,25 > 1 ⇒
1,5¹⁰⁰ = 2,25⁵⁰ > 2,25¹ > 2 ⇒
1,5¹⁰⁰ > 2 + log₂(3/4) ⇔
Похожие вопросы
Предмет: Алгебра,
автор: kakdelawery
Предмет: Химия,
автор: olesya280379
Предмет: Литература,
автор: kontik05224
Предмет: Математика,
автор: natina0309
Предмет: Алгебра,
автор: reizZer