Предмет: Алгебра,
автор: Immortal1000099
Найдите |b| если |a|=6 |a+b|=11 и |a-b|=7 все векторы a и b
Ответы
Автор ответа:
5
Попробуйте такое решение:1. Пусть координаты вектора "а" будут х_а и у_а, а координаты вектора 'b' - х_b и y_b соответственно.2. Используя координаты, можно составить три уравнения:- для длины вектора |a|: (х_а)²+(у_а)²=36 (по условию длина его 6);- для длины вектора |a+b|: (х_а+х_b)²+(y_a+y_b)²=121 (по условию его длина 11);- для длины вектора |a-b|: (x_a-x_b)²+(y_a-y_b)²=49 (по условию его длина равна 7).3. По трём уравнениям можно составить систему и решить её относительно [(x_b)²+(y_b)²]. Расчёты системы приведены во вложении (по возможности перепроверьте).Ответ: 7.
Приложения:
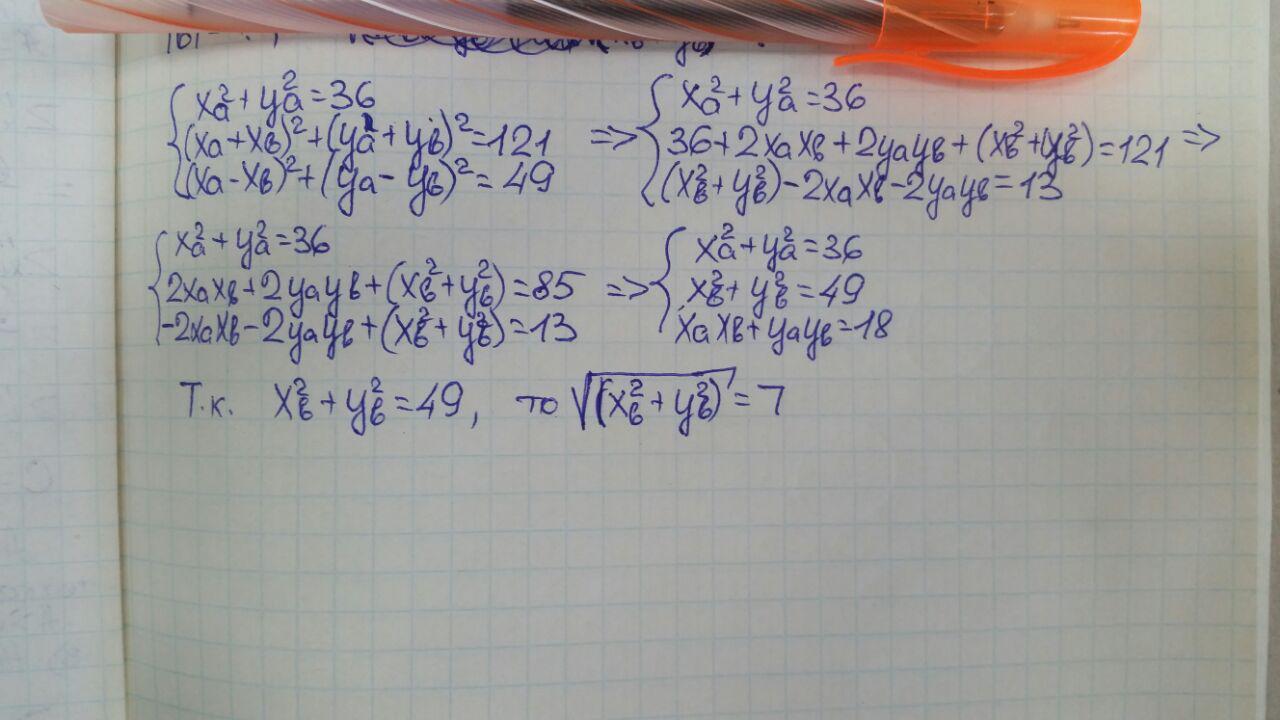
Похожие вопросы
Предмет: Алгебра,
автор: mnastia830
Предмет: Химия,
автор: michelleabigail999
Предмет: География,
автор: Evelinnas
Предмет: Информатика,
автор: Анабель666
Предмет: Математика,
автор: Nastenka3656