Предмет: Физика,
автор: 1ЛЗ
При малых колебаниях математического маятника длиной 0,5 м косинус максимального угла отклонения маятника от вертикали равен 0,9.
Какова скорость движения маятника в тот момент, когда косинус угла отклонения маятника от вертикали равен 0,949?
Ответы
Автор ответа:
3
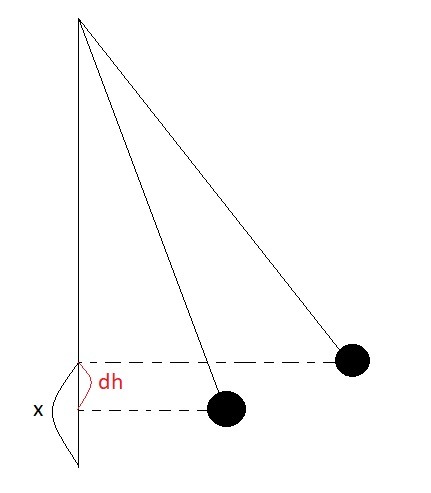
По закону сохранения энергии:  , где Δh - изменение высоты положения маятника при уменьшении угла. Косинус максимального угла:
, где Δh - изменение высоты положения маятника при уменьшении угла. Косинус максимального угла:
 ; При этом косинус угла, который дан в условии равен
; При этом косинус угла, который дан в условии равен  ; Зная при этом значение
; Зная при этом значение  находим значение Δh:
находим значение Δh:  , откуда
, откуда  ; Теперь находим значение скорости:
; Теперь находим значение скорости: 
Ответ: 0,7 м/с
Ответ: 0,7 м/с
Приложения:
Похожие вопросы
Предмет: Химия,
автор: Black1color
Предмет: Химия,
автор: kravchmaha45
Предмет: Биология,
автор: Аноним
Предмет: Математика,
автор: vikailen
Предмет: Литература,
автор: ЛФЕН