Предмет: Математика,
автор: laut2282015
Найти границы функции ,помогите!
Приложения:
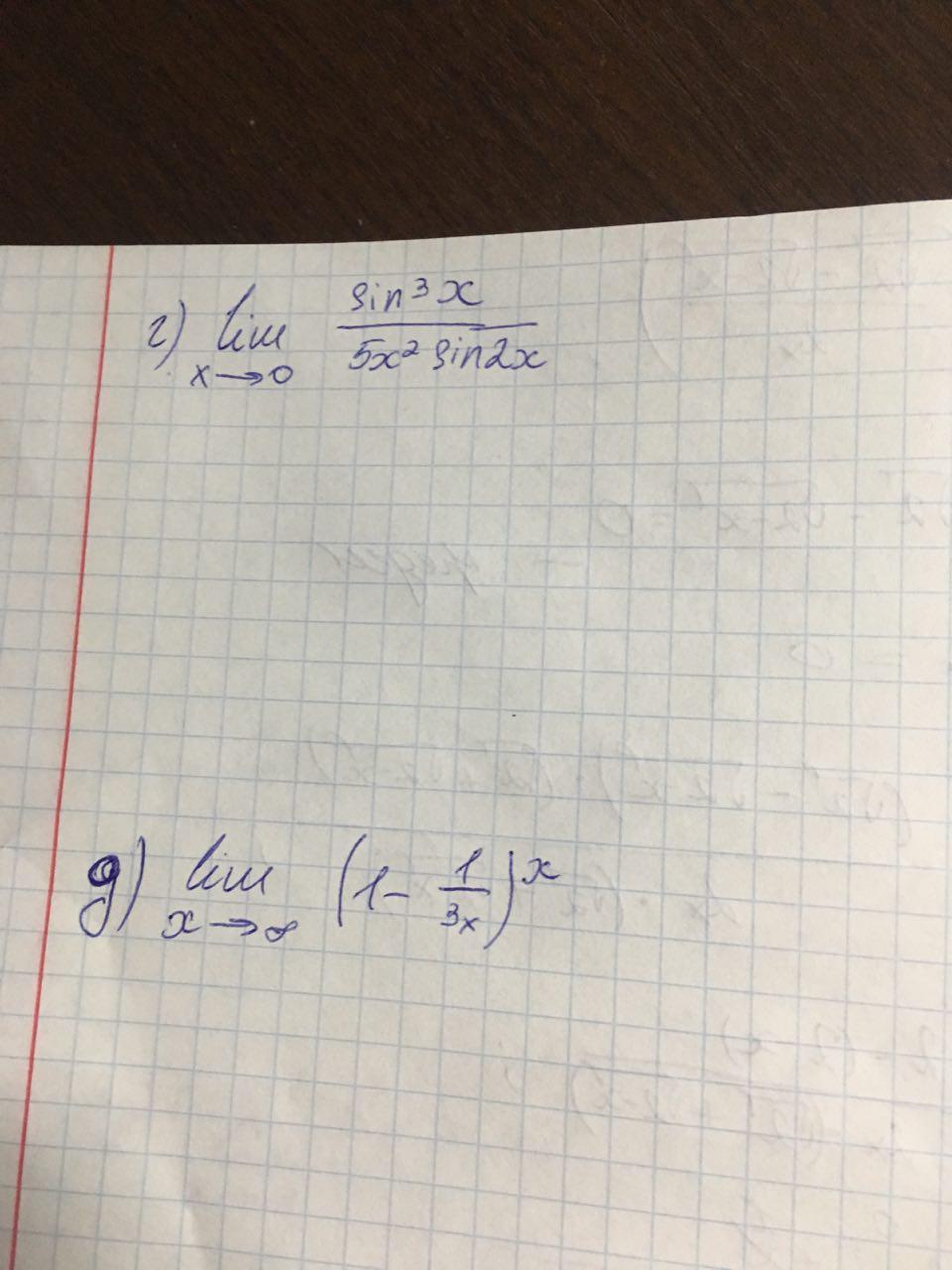
Ответы
Автор ответа:
0
lim (x->0)) (sin³x/(5x²sin2x)) = (sin2x=2sinxcosx)= lim (x->0) (sin³x/(5x²2sinxcosx)) = lim (x->0) (sin²x/(x²)*1/10cosx)) = (первое это замечательный первый предел lim(x->0) sinx/x=1) = 1²*1/(10cos(0)) = 1/10
lim(x->+∞) (1-1/3x)^x = lim(x->+∞) e^(ln(1-1/3x)^x) = lim(x->+∞) e^(xln(1-1/3x)) = e^ lim(x->+∞) (xln(1-1/3x)) = e^ lim(x->+∞) (ln(1-1/3x)/ (1/x)) = (получили неопределенность 0/0 раскрываем по Лопиталю, берем производные от числителя и знаменателя) = .......
lim(x->+∞) ln'(1-1/3x)/ (1/x)' = lim(x->+∞) 1/(3x²(1-1/3x)) / (-1/x²) =lim(x->+∞)- x/(3x-1) = lim(x->+∞) - x/x / (3x/x -1/x) = lim(x->+∞) - 1/(3 - 1/x) = -1/3
...... = e^ lim(x->+∞) (ln(1-1/3x)/ (1/x)) = e^(-1/3) = 1/∛e
lim(x->+∞) (1-1/3x)^x = lim(x->+∞) e^(ln(1-1/3x)^x) = lim(x->+∞) e^(xln(1-1/3x)) = e^ lim(x->+∞) (xln(1-1/3x)) = e^ lim(x->+∞) (ln(1-1/3x)/ (1/x)) = (получили неопределенность 0/0 раскрываем по Лопиталю, берем производные от числителя и знаменателя) = .......
lim(x->+∞) ln'(1-1/3x)/ (1/x)' = lim(x->+∞) 1/(3x²(1-1/3x)) / (-1/x²) =lim(x->+∞)- x/(3x-1) = lim(x->+∞) - x/x / (3x/x -1/x) = lim(x->+∞) - 1/(3 - 1/x) = -1/3
...... = e^ lim(x->+∞) (ln(1-1/3x)/ (1/x)) = e^(-1/3) = 1/∛e
Похожие вопросы
Предмет: Английский язык,
автор: rodionrazin2
Предмет: Русский язык,
автор: Аноним
Предмет: Английский язык,
автор: alexandra1853
Предмет: Математика,
автор: Аноним
Предмет: Литература,
автор: awer2210