Предмет: Геометрия,
автор: faku1
Найдите апофему, высоту, площадь полной поверхности и объем правильной четырехугольной пирамиды, у которой каждое ребро равно a. Построить пирамиду и развертку полной поверхности пирамиды.
Ответы
Автор ответа:
1
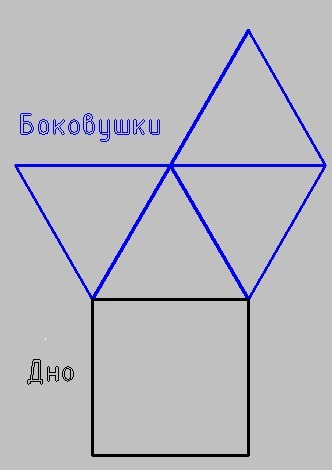
Развёртка есть :) Это самое простое.
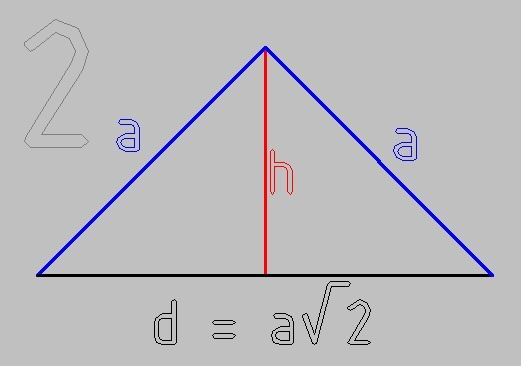
на рис.2 - диагональное сечение пирамиды, через диагональ основания и вершину
Диагональ основания по Пифагору
d² = a² + a²
d = a√2
стороны длиной а см
Видно, что это прямоугольный треугольник, точно такой же, как половинка основания
Его площадь через катеты
S = 1/2*a*a
Его площадь через гипотенузу и высоту к ней
S = 1/2*d*h
a*a = d*h
a² = a√2*h
h = a/√2 - это высота пирамиды
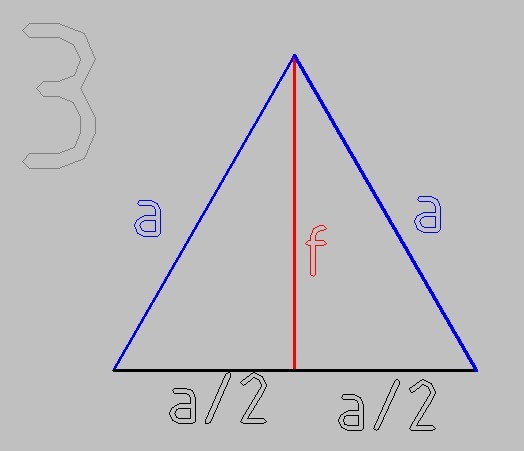
рис 3.
Боковая грань пирамиды представляет собой равносторонний треугольник - ведь все рёбра равны а
Для нахождения апофемы возьмём половину этого треугольника
По т. Пифагора
a² = (a/2)² + f²
f² = 3/4*a²
f = a√3/2
---
Площадь - это основание и 4 боковушки
S = a² + 4*1/2*a*f = a² + 2*a*a√3/2 = a²(1 + √3)
Объём
V = 1/3*a²*h = 1/3*a²*a/√2 = a³/(3√2)
на рис.2 - диагональное сечение пирамиды, через диагональ основания и вершину
Диагональ основания по Пифагору
d² = a² + a²
d = a√2
стороны длиной а см
Видно, что это прямоугольный треугольник, точно такой же, как половинка основания
Его площадь через катеты
S = 1/2*a*a
Его площадь через гипотенузу и высоту к ней
S = 1/2*d*h
a*a = d*h
a² = a√2*h
h = a/√2 - это высота пирамиды
рис 3.
Боковая грань пирамиды представляет собой равносторонний треугольник - ведь все рёбра равны а
Для нахождения апофемы возьмём половину этого треугольника
По т. Пифагора
a² = (a/2)² + f²
f² = 3/4*a²
f = a√3/2
---
Площадь - это основание и 4 боковушки
S = a² + 4*1/2*a*f = a² + 2*a*a√3/2 = a²(1 + √3)
Объём
V = 1/3*a²*h = 1/3*a²*a/√2 = a³/(3√2)
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: tiefgh
Предмет: Математика,
автор: skybogag33
Предмет: Биология,
автор: davidoffcomp
Предмет: История,
автор: здравствуйте47
Предмет: Математика,
автор: viktorpavlenko