Предмет: Алгебра,
автор: mayli
Вычислить двойной интеграл. Где область D - круговой сектор, ограниченный линиями (заданными ы в полярной системе координат)
Приложения:
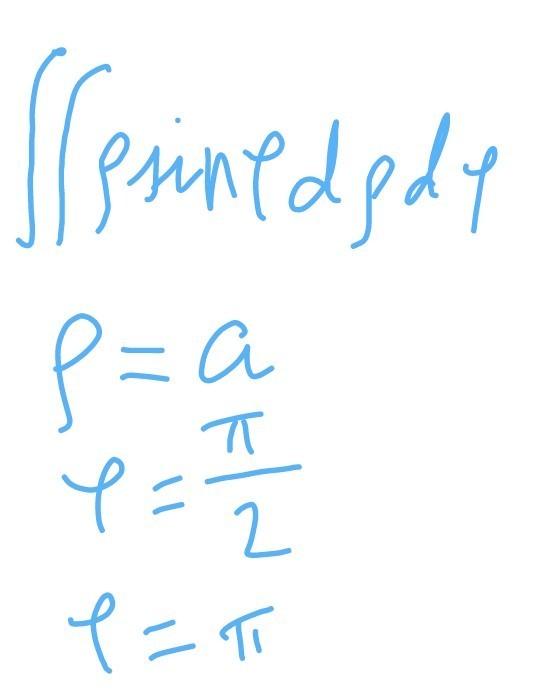
Ответы
Автор ответа:
0
Приложения:
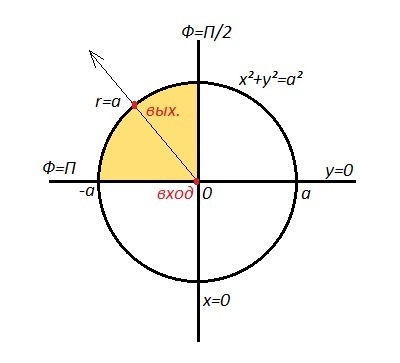
Похожие вопросы
Предмет: Українська література,
автор: kristinasamosina3
Предмет: Алгебра,
автор: DopustimA
Предмет: Физика,
автор: shnyrev00
Предмет: Алгебра,
автор: kraynovakarina
Предмет: Математика,
автор: antoninacherep